
【題目】教材曾有介紹:圓![]() 上的點
上的點![]() 處的切線方程為
處的切線方程為![]() 我們將其結論推廣:橢圓
我們將其結論推廣:橢圓![]() 的點
的點![]() 處的切線方程為
處的切線方程為![]() 在解本題時可以直接應用,已知直線
在解本題時可以直接應用,已知直線![]() 與橢圓E:
與橢圓E:![]() 有且只有一個公共點.
有且只有一個公共點.
(1)求![]() 的值;
的值;
(2)設O為坐標原點,過橢圓E上的兩點A、B分別作該橢圓的兩條切線![]() ,且
,且![]() 與
與![]() 交于點M
交于點M![]()
①設![]() ,直線AB、OM的斜率分別為
,直線AB、OM的斜率分別為![]() ,求證:
,求證:![]() 為定值;
為定值;
②設![]() ,求△OAB面積的最大值.
,求△OAB面積的最大值.
【答案】(1)![]() ;(2)證明見解析;②
;(2)證明見解析;②![]() .
.
【解析】
(1)將直線![]() 代入橢圓方程,得到
代入橢圓方程,得到![]() 的方程,由直線和橢圓相切的條件:判別式為0,解方程可得
的方程,由直線和橢圓相切的條件:判別式為0,解方程可得![]() 的值;
的值;
(2)①設切點![]() ,
,![]() ,
,![]() ,
,![]() ,可得切線
,可得切線![]() ,
,![]() ,再由
,再由![]() 代入上式,結合兩點確定一條直線,可得切點弦方程,即有
代入上式,結合兩點確定一條直線,可得切點弦方程,即有![]() 的斜率,結合兩點的斜率公式,即可得證;
的斜率,結合兩點的斜率公式,即可得證;
②由①可得![]() 的方程為
的方程為![]() ,運用點到直線的距離公式和直線與橢圓方程聯立,運用韋達定理和弦長公式,求得
,運用點到直線的距離公式和直線與橢圓方程聯立,運用韋達定理和弦長公式,求得![]() 的面積,化簡整理,運用基本不等式即可得到所求最大值.
的面積,化簡整理,運用基本不等式即可得到所求最大值.
解:(1)將直線![]() 代入橢圓方程
代入橢圓方程![]() ,
,
可得![]() ,
,
由直線和橢圓相切,可得△![]() ,
,
解得![]() (由
(由![]() ;
;

(2)①證明:設切點![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可得切線![]() ,
,![]() ,
,
由![]() 與
與![]() 交于點
交于點![]() ,可得
,可得![]() ,
,![]() ,
,
由兩點確定一條直線,可得![]() 的方程為
的方程為![]() ,即為
,即為![]() ,
,
即有![]() ,
,![]() ,可得
,可得![]() 為定值
為定值![]() ;
;
②由①可得![]() 的方程為
的方程為![]() ,
,
原點到直線![]() 的距離為
的距離為![]() ,
,
由![]() 消去
消去![]() ,可得
,可得![]() ,
,
![]() ,
,![]() ,
,
可得![]()
![]()
![]() ,
,
可得![]() 的面積
的面積![]() ,
,
設![]() ,
,
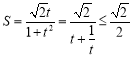 ,
,
當且僅當![]() 即
即![]() 時,
時,![]() 取得最大值
取得最大值![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知點F為拋物線C:![]() (
(![]() )的焦點,過點F的動直線l與拋物線C交于M,N兩點,且當直線l的傾斜角為45°時,
)的焦點,過點F的動直線l與拋物線C交于M,N兩點,且當直線l的傾斜角為45°時,![]() .
.
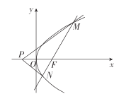
(1)求拋物線C的方程.
(2)試確定在x軸上是否存在點P,使得直線PM,PN關于x軸對稱?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在全國第五個“扶貧日”到來之前,某省開展“精準扶貧,攜手同行”的主題活動,某貧困縣調查基層干部走訪貧困戶數量.甲鎮有基層干部60人,乙鎮有基層干部60人,丙鎮有基層干部80人,每人都走訪了若干貧困戶,按照分層抽樣,從甲、乙、丙三鎮共選20名基層干部,統計他們走訪貧困戶的數量,并將走訪數量分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5組,繪制成如圖所示的頻率分布直方圖.
5組,繪制成如圖所示的頻率分布直方圖.
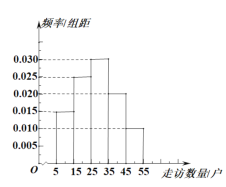
(1)求這20人中有多少人來自丙鎮,并估計甲、乙、丙三鎮的基層干部走訪貧困戶戶數的中位數(精確到整數位);
(2)如果把走訪貧困戶達到或超過35戶視為工作出色,求選出的20名基層干部中工作出色的人數,并從中選2人做交流發言,求這2人中至少有一人走訪的貧困戶在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電視臺舉行文藝比賽,并通過網絡對比賽進行直播.比賽現場有5名專家評委給每位參賽選手評分,場外觀眾可以通過網絡給每位參賽選手評分.每位選手的最終得分由專家評分和觀眾評分確定.某選手參與比賽后,現場專家評分情況如表;場外有數萬名觀眾參與評分,將評分按照[7,8),[8,9),[9,10]分組,繪成頻率分布直方圖如圖:
專家 | A | B | C | D | E |
評分 | 9.6 | 9.5 | 9.6 | 8.9 | 9.7 |
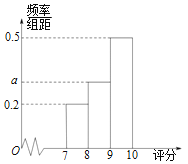
(1)求a的值,并用頻率估計概率,估計某場外觀眾評分不小于9的概率;
(2)從5名專家中隨機選取3人,X表示評分不小于9分的人數;從場外觀眾中隨機選取3人,用頻率估計概率,Y表示評分不小于9分的人數;試求E(X)與E(Y)的值;
(3)考慮以下兩種方案來確定該選手的最終得分:方案一:用所有專家與觀眾的評分的平均數![]() 作為該選手的最終得分,方案二:分別計算專家評分的平均數
作為該選手的最終得分,方案二:分別計算專家評分的平均數![]() 和觀眾評分的平均數
和觀眾評分的平均數![]() ,用
,用![]() 作為該選手最終得分.請直接寫出
作為該選手最終得分.請直接寫出![]() 與
與![]() 的大小關系.
的大小關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義“矩陣”的一種運算![]() ,該運算的意義為點
,該運算的意義為點![]() 在矩陣的變換下成點
在矩陣的變換下成點![]() 設矩陣
設矩陣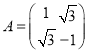
![]() 已知點
已知點![]() 在矩陣
在矩陣![]() 的變換后得到的點
的變換后得到的點![]() 的坐標為
的坐標為![]() ,試求點
,試求點![]() 的坐標;
的坐標;
![]() 是否存在這樣的直線:它上面的任一點經矩陣
是否存在這樣的直線:它上面的任一點經矩陣![]() 變換后得到的點仍在該直線上?若存在,試求出所有這樣的直線;若不存在,則說明理由.
變換后得到的點仍在該直線上?若存在,試求出所有這樣的直線;若不存在,則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知空間幾何體![]() 中,
中,![]() 與
與![]() 均為邊長為
均為邊長為![]() 的等邊三角形,
的等邊三角形,![]() 為腰長為
為腰長為![]() 的等腰三角形,平面
的等腰三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
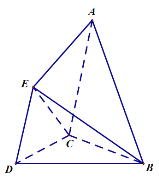
(1)試在平面![]() 內作一條直線,使直線上任意一點
內作一條直線,使直線上任意一點![]() 與
與![]() 的連線
的連線![]() 均與平面
均與平面![]() 平行,并給出詳細證明;
平行,并給出詳細證明;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com