
【題目】已知函數f(x)=ax﹣ ![]() (a,b∈N*),f(1)=
(a,b∈N*),f(1)= ![]() 且f(2)<2.
且f(2)<2.
(Ⅰ)求a,b的值;
(Ⅱ)判斷并證明函數y=f(x)在區間(﹣1,+∞)上的單調性.
【答案】解:(Ⅰ)∵ ![]() ,
, ![]() ,
,
由 ![]() ,
,
∴ ![]() ,
,
又∵a,b∈N* ,
∴b=1,a=1;
(Ⅱ)由(1)得 ![]() ,
,
函數在(﹣1,+∞)單調遞增.
證明:任取x1 , x2且﹣1<x1<x2 , ![]()
= ![]() ,
,
∵﹣1<x1<x2 ,
∴ ![]() ,
,
∴ ![]() ,
,
即f(x1)<f(x2),
故函數 ![]() 在(﹣1,+∞)上單調遞增
在(﹣1,+∞)上單調遞增
【解析】(Ⅰ)由 ![]() ,
, ![]() ,
, ![]() ,從而求出b=1,a=1;(Ⅱ)由(1)得
,從而求出b=1,a=1;(Ⅱ)由(1)得 ![]() ,得函數在(﹣1,+∞)單調遞增.從而有f(x1 )﹣f(x2 )=
,得函數在(﹣1,+∞)單調遞增.從而有f(x1 )﹣f(x2 )= ![]() ,進而
,進而 ![]() ,故函數
,故函數 ![]() 在(﹣1,+∞)上單調遞增.
在(﹣1,+∞)上單調遞增.
【考點精析】關于本題考查的利用導數研究函數的單調性,需要了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減才能得出正確答案.
在這個區間單調遞減才能得出正確答案.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩名選手參加歌手大賽時,5名評委打的分數用莖葉圖表示(如圖).s1、s2分別表示甲、乙選手分數的標準差,則s1與s2的關系是( ) 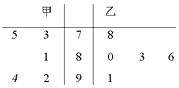
A.s1>s2
B.s1=s2
C.s1<s2
D.不確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐S﹣ABCD中,底面ABCD為平行四邊形,AB=3,AC=4,AD=5,SA⊥平面ABCD. 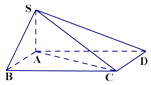
(1)證明:AC⊥平面SAB;
(2)若SA=2,求三棱錐A﹣SCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】排列組合
(1)7位同學站成一排,甲、乙兩同學必須相鄰的排法共有多少種?
(2)7位同學站成一排,甲、乙和丙三個同學都不能相鄰的排法共有多少種?
(3)7位同學站成一排,甲不站排頭,乙不站排尾,不同站法種數有多少種?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com