
若點 和點
和點 分別為雙曲線
分別為雙曲線 (
( )的中心和左焦點,點
)的中心和左焦點,點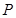 為雙曲線右支上的任意一點,則
為雙曲線右支上的任意一點,則 的取值范圍為( )
的取值范圍為( )
A.[3-  , ,  ) ) | B.[3+  , ,  ) ) |
C.[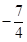 , ,  ) ) | D.[ , ,  ) ) |
B
解析試題分析: 因為F(-2,0)是已知雙曲線的左焦點,所以a2+1=4,即a2=3,所以雙曲線方程為 設點P(x0,y0),則有
設點P(x0,y0),則有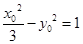 (x0≥
(x0≥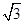 ),解得y02=
),解得y02= (x0≥
(x0≥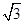 ),
),
因為 =(x0+2,y0),
=(x0+2,y0),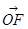 =(x0,y0),所以
=(x0,y0),所以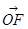
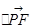 =x0(x0+2)+y02=x0(x0+2)+
=x0(x0+2)+y02=x0(x0+2)+ =
= +2x0-1,此二次函數對應的拋物線的對稱軸為x0=-
+2x0-1,此二次函數對應的拋物線的對稱軸為x0=-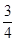 ,因為x0≥
,因為x0≥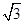 ,
,
所以當x0=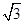 時,
時,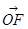
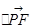 取得最小值
取得最小值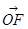
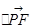 =
= ,故
,故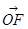
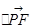
的取值范圍是[ ,+∞),選B
,+∞),選B
考點:本題主要考查了待定系數法求雙曲線方程,考查平面向量的數量積的坐標運算、二次函數的單調性與最值等,考查了同學們對基礎知識的熟練程度以及知識的綜合應用能力、運算能力.
點評:解決該試題的關鍵是先根據雙曲線的焦點和方程中的b求得a,則雙曲線的方程可得,設出點P,代入雙曲線方程求得y0的表達式,根據P,F,O的坐標表示出 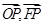 ,進而求得
,進而求得  的表達式,利用二次函數的性質求得其最小值,則
的表達式,利用二次函數的性質求得其最小值,則 的取值范圍可得.
的取值范圍可得.


 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:單選題
已知雙曲線 (a>0,b>0)的一條漸近線方程是y=
(a>0,b>0)的一條漸近線方程是y= x,它的一個焦點在拋物線y2=24x的準線上,則雙曲線的方程為( )
x,它的一個焦點在拋物線y2=24x的準線上,則雙曲線的方程為( )
A. | B. |
C. | D. |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
對于平面直角坐標系內的任意兩點 ,定義它們之間的一種“距離”:
,定義它們之間的一種“距離”: .給出下列三個命題:
.給出下列三個命題:
①若點C在線段AB上,則 ;
;
②在 中,若∠C=90°,則
中,若∠C=90°,則 ;
;
③在 中,
中, .
.
其中真命題的個數為( )
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com