
【題目】已知橢圓C1: ![]() +
+ ![]() =1(a>b>0)過點A(1,
=1(a>b>0)過點A(1, ![]() ),其焦距為2.
),其焦距為2. 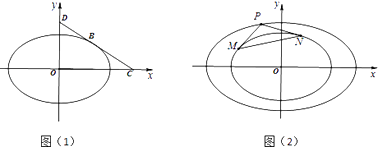
(1)求橢圓C1的方程;
(2)已知橢圓具有如下性質:若橢圓的方程為 ![]() +
+ ![]() =1(a>b>0),則橢圓在其上一點A(x0 , y0)處的切線方程為
=1(a>b>0),則橢圓在其上一點A(x0 , y0)處的切線方程為 ![]() +
+ ![]() =1,試運用該性質解決以下問題:
=1,試運用該性質解決以下問題:
(i)如圖(1),點B為C1在第一象限中的任意一點,過B作C1的切線l,l分別與x軸和y軸的正半軸交于C,D兩點,求△OCD面積的最小值;
(ii)如圖(2),過橢圓C2: ![]() +
+ ![]() =1上任意一點P作C1的兩條切線PM和PN,切點分別為M,N.當點P在橢圓C2上運動時,是否存在定圓恒與直線MN相切?若存在,求出圓的方程;若不存在,請說明理由.
=1上任意一點P作C1的兩條切線PM和PN,切點分別為M,N.當點P在橢圓C2上運動時,是否存在定圓恒與直線MN相切?若存在,求出圓的方程;若不存在,請說明理由.
【答案】
(1)解:依題意得:橢圓的焦點為F1(﹣1,0),F2(1,0),由橢圓定義知:2a=|AF1|+|AF2|,
∴ ![]() ,所以橢圓C1的方程為
,所以橢圓C1的方程為 ![]() .
.
(2)解:(ⅰ)設B(x2,y2),則橢圓C1在點B處的切線方程為 ![]()
令x=0, ![]() ,令
,令 ![]() ,所以
,所以 ![]()
又點B在橢圓的第一象限上,所以 ![]() ,
,
∴ ![]()
∴ ![]() ,當且僅當
,當且僅當 ![]()
所以當 ![]() 時,三角形OCD的面積的最小值為
時,三角形OCD的面積的最小值為 ![]()
(ii)設P(m,n),則橢圓C1在點M(x3,y3)處的切線為: ![]()
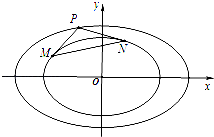
又PM過點P(m,n),所以 ![]() ,同理點N(x4,y4)也滿足
,同理點N(x4,y4)也滿足 ![]() ,
,
所以M,N都在直線 ![]() 上,
上,
即:直線MN的方程為 ![]()
所以原點O到直線MN的距離 ![]() =
= ![]() ,
,
所以直線MN始終與圓 ![]() 相切.
相切.
【解析】(1)依題意得:橢圓的焦點為F1(﹣1,0),F2(1,0),由橢圓定義知:2a=|AF1|+|AF2|,即可求出a,b,從而可求橢圓C1的方程;(2)(i)確定 ![]() ,再結合基本不等式,即可求△OCD面積的最小值;(ii)先求出直線MN的方程,再求出原點O到直線MN的距離,即可得出結論.
,再結合基本不等式,即可求△OCD面積的最小值;(ii)先求出直線MN的方程,再求出原點O到直線MN的距離,即可得出結論.


科目:高中數學 來源: 題型:
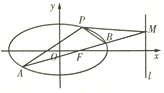
【題目】如圖,橢圓![]() 經過點
經過點![]() ,離心率
,離心率![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
![]() 求橢圓
求橢圓![]() 的方程;
的方程;
![]()
![]() 是經過右焦點
是經過右焦點![]() 的任一弦(不經過點
的任一弦(不經過點![]() ),設直線
),設直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,記
,記![]() ,
, ![]() ,
, ![]() 的斜率為
的斜率為![]() ,
, ![]() ,
, ![]() .問:是否存在常數
.問:是否存在常數![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數 ![]()
(1)若b和c分別是先后拋擲一枚骰子得到的點數,求對任意x∈R,f(x)>0恒成立的概率.
(2)若b是從區間[0,8](3)任取得一個數,c是從[0,6]任取的一個數,求函數f(x)的圖象與x軸有交點的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4一4:坐標系與參數方程
已知曲線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)寫出![]() 的極坐標方程和
的極坐標方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 的極坐標分別為
的極坐標分別為![]() 和
和![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,射線
兩點,射線![]()
與曲線![]() 相交于點
相交于點![]() ,射線
,射線![]() 與曲線
與曲線![]() 相交于點
相交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com