【題目】已知函數(shù)
(
為自然對數(shù)的底數(shù)).
(Ⅰ)求函數(shù)
的單調(diào)區(qū)間；
(Ⅱ)若
，
，試求函數(shù)
極小值的最大值.
【答案】（1）單調(diào)遞減區(qū)間是
，單調(diào)遞增區(qū)間是
； （2）1.
【解析】
（I）計算
導(dǎo)函數(shù)，構(gòu)造函數(shù)
，判定單調(diào)性，得到的單調(diào)性，即可。（II）得到
的解析式，結(jié)合導(dǎo)函數(shù)判定單調(diào)性，得到極小值，構(gòu)造函數(shù)
，結(jié)合導(dǎo)函數(shù)，計算該函數(shù)的極值，即可。
(Ⅰ)易知
，且
.
令
，則
，
∴函數(shù)在
上單調(diào)遞增，且
.
可知，當(dāng)
時，
，
單調(diào)遞減；
當(dāng)
時，
，單調(diào)遞增.
∴函數(shù)的單調(diào)遞減區(qū)間是
，單調(diào)遞增區(qū)間是.
(Ⅱ)∵
，∴
.
由(Ⅰ)知，
在上單調(diào)遞增，
當(dāng)
時，
；當(dāng)
時，
，則
有唯一解
.
可知，當(dāng)
時，
，
單調(diào)遞減；
當(dāng)
時，
，單調(diào)遞增，
∴函數(shù)在
處取得極小值
，且滿足
.
∴
.
令
，則
.
可知，當(dāng)時，
，單調(diào)遞增；
當(dāng)時，
，單調(diào)遞減，
∴
.
∴函數(shù)極小值的最大值為1.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】中央政府為了應(yīng)對因人口老齡化而造成的勞動力短缺等問題，擬定出臺“延遲退休年齡政策”為了了解人們對“延遲退休年齡政策”的態(tài)度，責(zé)成人社部進行調(diào)研．人社部從網(wǎng)上年齡在15-65歲的人群中隨機調(diào)查100人，調(diào)查數(shù)據(jù)的頻率分布直方圖和支持“延遲退休”的人數(shù)與年齡的統(tǒng)計結(jié)果如下：
年齡 |
|
|
|
|
|
支持“延遲退休”的人數(shù) | 15 | 5 | 15 | 28 | 17 |
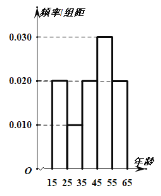
（1）由以上統(tǒng)計數(shù)據(jù)填2×2列聯(lián)表，并判斷能否在犯錯誤的概率不超過0．05的前提下認為以45歲為分界點的不同人群對“延遲退休年齡政策”的支持度有差異；
45歲以下 | 45歲以上 | 總計 | |
支持 | |||
不支持 | |||
總計 |
參考數(shù)據(jù)：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
，其中
．
（2）若以45歲為分界點，從不支持“延遲退休”的人中按分層抽樣的方法抽取8人參加某項活動、現(xiàn)從這8人中隨機抽2人．記抽到45歲以上的人數(shù)為X，求隨機變量X的分布列及數(shù)學(xué)期望．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某學(xué)校實行自主招生，參加自主招生的學(xué)生從8個試題中隨機挑選出4個進行作答，至少答對3個才能通過初試，已知甲、乙兩人參加初試，在這8個試題中甲能答對6個，乙能答對每個試題的概率為
，且甲、乙兩人是否答對每個試題互不影響.
（1）試通過概率計算，分析甲、乙兩人誰通過自主招生初試的可能性更大；
（2）若答對一題得5分，答錯或不答得0分，記乙答題的得分為
，求的分布列.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）＝aex﹣2x+1．
（1）當(dāng)a＝1時，求函數(shù)f（x）的極值；
（2）若f（x）＞0對x∈R成立，求實數(shù)a的取值范圍
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】金秋九月，丹桂飄香，某高校迎來了一大批優(yōu)秀的學(xué)生．新生接待其實也是和社會溝通的一個平臺．校團委、學(xué)生會從在校學(xué)生中隨機抽取了160名學(xué)生，對是否愿意投入到新生接待工作進行了問卷調(diào)查，統(tǒng)計數(shù)據(jù)如下：
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
（1）根據(jù)上表說明，能否有99%把握認為愿意參加新生接待工作與性別有關(guān)；
（2）現(xiàn)從參與問卷調(diào)查且愿意參加新生接待工作的學(xué)生中，采用按性別分層抽樣的方法，選取10人．若從這10人中隨機選取3人到火車站迎接新生，設(shè)選取的3人中女生人數(shù)為
，寫出的分布列，并求
．
附：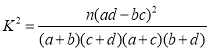
，其中
．
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某公司為確定下一年度投入某種產(chǎn)品的宣傳費，需了解年宣傳費
(單位：千元)對年銷售量
(單位：
)和年利潤
(單位：千元)的影響.對近
年的年宣傳費
和年銷售量數(shù)據(jù)
作了初步處理，得到下面的散點圖及一些統(tǒng)計量的值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中
，
.附：對于一組數(shù)據(jù)
，
，
，
，其回歸直線
的斜率和截距的最小二乘法估計分別為
，
.
（1）根據(jù)散點圖判斷，
與
在哪一個適宜作為年銷售量 關(guān)于年宣傳費 的回歸方程類型？(給出判斷即可，不必說明理由)
（2）根據(jù)1小問的判斷結(jié)果及表中數(shù)據(jù)，建立 關(guān)于 的回歸方程；
（3）已知這種產(chǎn)品的年利潤 與
的關(guān)系為
.根據(jù)2小問的結(jié)果回答下列問題：
①2年宣傳費
時，年銷售量及年利潤的預(yù)報值是多少？
②3年宣傳費為何值時，年利潤的預(yù)報值最大？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（
，
是自然對數(shù)的底數(shù)）
(Ⅰ) 設(shè)
（其中
是
的導(dǎo)數(shù)），求
的極小值；
(Ⅱ) 若對
，都有
成立，求實數(shù)
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
