
【題目】在平行四邊形![]() 中,
中,![]() ,
,![]() ,過
,過![]() 點作
點作![]() 的垂線,交
的垂線,交![]() 的延長線于點
的延長線于點![]() ,
,![]() .連結(jié)
.連結(jié)![]() ,交
,交![]() 于點
于點![]() ,如圖1,將
,如圖1,將![]() 沿
沿![]() 折起,使得點
折起,使得點![]() 到達點
到達點![]() 的位置,如圖2.
的位置,如圖2.
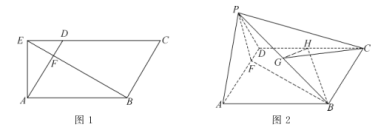
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點,且平面
的中點,且平面![]() 平面
平面![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
【答案】(1)見解析; (2)![]() .
.
【解析】
(1)先求得![]() ,
,![]() ,可得
,可得![]() ,結(jié)合
,結(jié)合![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,可證明
,可證明![]() 平面
平面![]() ,利用面面垂直的判定定理可得平面
,利用面面垂直的判定定理可得平面![]() 平面
平面![]() ;(2)由面面垂直的性質(zhì)可得
;(2)由面面垂直的性質(zhì)可得![]() 平面
平面![]() ,取
,取![]() 的中點為
的中點為![]() ,連結(jié)
,連結(jié)![]() ,則
,則![]() ,可證明
,可證明![]() 平面
平面![]() ,由此利用棱錐的體積公式可得三棱錐
,由此利用棱錐的體積公式可得三棱錐![]() 的體積.
的體積.
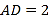
(1)如題圖1,在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() .
.
在![]() 中,
中,![]() ,所以
,所以![]() .
.
所以![]() .
.
如題圖2,![]() ,
,![]() .又因為
.又因為![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,又因為
,又因為![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解法一:因為平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
取![]() 的中點為
的中點為![]() ,連結(jié)
,連結(jié)![]() ,則
,則![]() ,所以
,所以![]() 平面
平面![]() .
.
即![]() 為三棱錐
為三棱錐![]() 的高.
的高.
且![]() .
.
因為,三棱錐![]() 的體積為
的體積為![]() .
.

解法二:因為平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
,所以![]() 平面
平面![]() .
.
因為![]() 為
為![]() 的中點.
的中點.
所以三棱錐![]() 的高等于
的高等于![]() .
.
因為![]() 為
為![]() 的中點,所以
的中點,所以![]() 的面積是四邊形
的面積是四邊形![]() 的面積的
的面積的![]() ,
,
從而三棱錐![]() 的體積是四棱錐
的體積是四棱錐![]() 的體積的
的體積的![]() .
.
面![]() ,
,
所以三棱錐![]() 的體積為
的體積為![]() .
.


 優(yōu)質(zhì)課堂快樂成長系列答案
優(yōu)質(zhì)課堂快樂成長系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
,![]() .
.
(1)若曲線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸平行,求
軸平行,求![]() ;
;
(2)當![]() 時,函數(shù)
時,函數(shù)![]() 的圖象恒在
的圖象恒在![]() 軸上方,求
軸上方,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】趙爽是我國古代數(shù)學(xué)家、天文學(xué)家,大約在公元222年,趙爽為《周髀算經(jīng)》一書作序時,介紹了“勾股圓方圖”,亦稱“趙爽弦圖”(以弦為邊長得到的正方形由4個全等的直角三角形再加上中間的一個小正方形組成的),類比“趙爽弦圖”,可類似地構(gòu)造如圖所示的圖形,它是由3個全等的三角形與中間的一個小等邊三角形拼成的一個大等邊三角形,設(shè)![]() ,則( )
,則( )
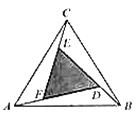
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)當![]() 時,判斷函數(shù)
時,判斷函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)當![]() 時,證明:
時,證明:![]() .(
.(![]() 為自然對數(shù)的底數(shù))
為自然對數(shù)的底數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形ABCD中,![]() ,E為AB的中點.將
,E為AB的中點.將![]() 沿DE翻折,得到四棱錐
沿DE翻折,得到四棱錐![]() .設(shè)
.設(shè)![]() 的中點為M,在翻折過程中,有下列三個命題:
的中點為M,在翻折過程中,有下列三個命題:
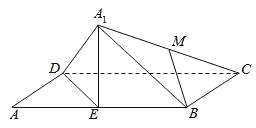
①總有![]() 平面
平面![]() ;
;
②線段BM的長為定值;
③存在某個位置,使DE與![]() 所成的角為90°.
所成的角為90°.
其中正確的命題是_______.(寫出所有正確命題的序號)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為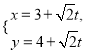 (
(![]() 為參數(shù)),以坐標原點為極點,
為參數(shù)),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,并使得它與直角坐標系
軸的正半軸為極軸建立極坐標系,并使得它與直角坐標系![]() 有相同的長度單位,曲線
有相同的長度單位,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設(shè)曲線![]() 與直線
與直線![]() 交于
交于![]() 、
、![]() 兩點,且
兩點,且![]() 點的坐標為
點的坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() 為參數(shù)),以坐標原點為極點,
為參數(shù)),以坐標原點為極點,![]() 軸為極軸建立極坐標系,曲線
軸為極軸建立極坐標系,曲線![]() .
.
(1)求曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)求與直線![]() 平行,且被曲線
平行,且被曲線![]() 截得的弦長為
截得的弦長為![]() 的直線
的直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知過定點![]() 且與直線
且與直線![]() 垂直的直線與
垂直的直線與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() ,點
,點 滿足
滿足![]() .
.
(1)若以原點為圓心的圓![]() 與
與![]() 有唯一公共點,求圓
有唯一公共點,求圓![]() 的軌跡方程;
的軌跡方程;
(2)求能覆蓋![]() 的最小圓的面積;
的最小圓的面積;
(3)在(1)的條件下,點![]() 在直線
在直線![]() 上,圓
上,圓![]() 上總存在兩個不同的點
上總存在兩個不同的點![]() 使得
使得![]()
![]() 為坐標原點),求
為坐標原點),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為研究男、女生的身高差異,現(xiàn)隨機從高二某班選出男生、女生各![]() 人,并測量他們的身高,測量結(jié)果如下(單位:厘米):
人,并測量他們的身高,測量結(jié)果如下(單位:厘米):
男:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
女:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 根據(jù)測量結(jié)果完成身高的莖葉圖(單位:厘米),并分別求出男、女生身高的平均值.
根據(jù)測量結(jié)果完成身高的莖葉圖(單位:厘米),并分別求出男、女生身高的平均值.
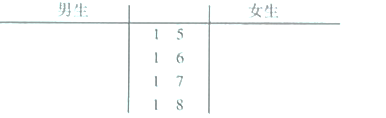
![]() 請根據(jù)測量結(jié)果得到
請根據(jù)測量結(jié)果得到![]() 名學(xué)生身高的中位數(shù)中位數(shù)
名學(xué)生身高的中位數(shù)中位數(shù)![]() (單位:厘米),將男、女身高不低于
(單位:厘米),將男、女身高不低于![]() 和低于
和低于![]() 的人數(shù)填入下表中,并判斷是否有
的人數(shù)填入下表中,并判斷是否有![]() 的把握認為男、女身高有差異?
的把握認為男、女身高有差異?

參照公式:![]()

![]() 若男生身高低于165厘米為偏矮,不低于165厘米且低于175厘米為正常,不低于175厘米為偏高,假設(shè)可以用測量結(jié)果的頻率代替概率,試求從高三的男生中任意選出2人,恰有1人身高屬于正常的概率.
若男生身高低于165厘米為偏矮,不低于165厘米且低于175厘米為正常,不低于175厘米為偏高,假設(shè)可以用測量結(jié)果的頻率代替概率,試求從高三的男生中任意選出2人,恰有1人身高屬于正常的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com