
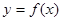 的圖象關于直線
的圖象關于直線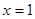 對稱,且當
對稱,且當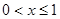 時,
時,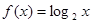 ,則方程
,則方程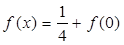 在區間
在區間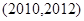 內的所有實數根之和為( )
內的所有實數根之和為( )| A.4020 | B.4022 | C.4024 | D.4026 |
 ,∴f(x)=
,∴f(x)= ,∵0<x≤1時,f(x)=log2x≤0,∴f(x)=
,∵0<x≤1時,f(x)=log2x≤0,∴f(x)= 在(0,1)內沒有一實根,在(-1,0)內有一實數根x1,又函數f(x)的圖象關于直線x=1對稱,∴f(x)=
在(0,1)內沒有一實根,在(-1,0)內有一實數根x1,又函數f(x)的圖象關于直線x=1對稱,∴f(x)= 在(2,3)有一個實根x2,且x1+x2=2;
在(2,3)有一個實根x2,且x1+x2=2;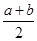 =2011∴a+b=4022,故選B2x與奇函數f(x)的圖象關于直線x=1對稱,數形結合予以解決,屬于中檔題.
=2011∴a+b=4022,故選B2x與奇函數f(x)的圖象關于直線x=1對稱,數形結合予以解決,屬于中檔題. +f(0)=
+f(0)= 在區間(2010,20121)內的所有實根之和.
在區間(2010,20121)內的所有實根之和.

 優加精卷系列答案
優加精卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com