
已知集合 ,其中
,其中 ,由
,由 中的元素構(gòu)成兩個相應(yīng)的集合:
中的元素構(gòu)成兩個相應(yīng)的集合:
 ,
, .
.
其中 是有序數(shù)對,集合
是有序數(shù)對,集合 和
和 中的元素個數(shù)分別為
中的元素個數(shù)分別為 和
和 .
.
若對于任意的 ,總有
,總有 ,則稱集合
,則稱集合 具有性質(zhì)
具有性質(zhì) .
.
(I)檢驗(yàn)集合 與
與 是否具有性質(zhì)
是否具有性質(zhì) 并對其中具有性質(zhì)
并對其中具有性質(zhì) 的集合,寫出相應(yīng)的集合
的集合,寫出相應(yīng)的集合 和
和 ;
;
(II)對任何具有性質(zhì) 的集合
的集合 ,證明:
,證明: ;
;
(III)判斷 和
和 的大小關(guān)系,并證明你的結(jié)論.
的大小關(guān)系,并證明你的結(jié)論.
(I)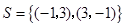 ;
;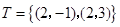
(II)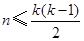
(III)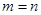
【解析】解:集合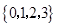 不具有性質(zhì)
不具有性質(zhì)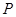 .
.
集合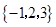 具有性質(zhì)
具有性質(zhì)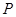 ,其相應(yīng)的集合
,其相應(yīng)的集合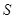 和
和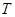 是
是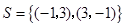 ,
,
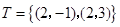 .
.
(II)證明:首先,由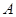 中元素構(gòu)成的有序數(shù)對
中元素構(gòu)成的有序數(shù)對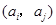 共有
共有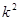 個.
個.
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012051810415951565809/SYS201205181043177656383747_DA.files/image013.png">,所以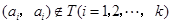 ;
;
又因?yàn)楫?dāng)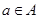 時,
時,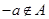 時,
時,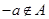 ,所以當(dāng)
,所以當(dāng)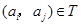 時,
時,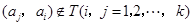 .
.
從而,集合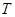 中元素的個數(shù)最多為
中元素的個數(shù)最多為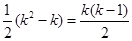 ,
,
即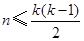 .
.
(III)解: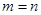 ,證明如下:
,證明如下:
(1)對于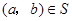 ,根據(jù)定義,
,根據(jù)定義,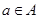 ,
,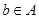 ,且
,且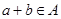 ,從而
,從而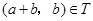 .
.
如果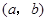 與
與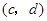 是
是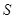 的不同元素,那么
的不同元素,那么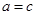 與
與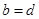 中至少有一個不成立,從而
中至少有一個不成立,從而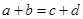 與
與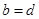 中也至少有一個不成立.
中也至少有一個不成立.
故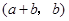 與
與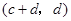 也是
也是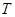 的不同元素.
的不同元素.
可見,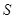 中元素的個數(shù)不多于
中元素的個數(shù)不多于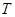 中元素的個數(shù),即
中元素的個數(shù),即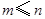 ,
,
(2)對于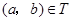 ,根據(jù)定義,
,根據(jù)定義,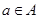 ,
,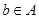 ,且
,且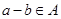 ,從而
,從而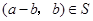 .如果
.如果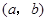 與
與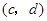 是
是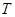 的不同元素,那么
的不同元素,那么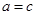 與
與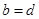 中至少有一個不成立,從而
中至少有一個不成立,從而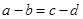 與
與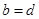 中也不至少有一個不成立,
中也不至少有一個不成立,
故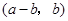 與
與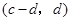 也是
也是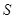 的不同元素.
的不同元素.
可見,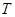 中元素的個數(shù)不多于
中元素的個數(shù)不多于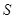 中元素的個數(shù),即
中元素的個數(shù),即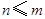 ,
,
由(1)(2)可知,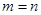 .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:044
(2007
北京,20)已知集合 ,其中
,其中 .由A中的元素構(gòu)成兩個相應(yīng)的集合:
.由A中的元素構(gòu)成兩個相應(yīng)的集合: ;
; ,其中(a,b)是有序數(shù)對.集合S和T中的元素個數(shù)分別為m和n.
,其中(a,b)是有序數(shù)對.集合S和T中的元素個數(shù)分別為m和n.
若對于任意的
 ,總有
,總有 ,則稱集合A具有性質(zhì)P.
,則稱集合A具有性質(zhì)P.
(1)
檢驗(yàn)集合{0,l,2,3}與{-1,2,3}是否具有性質(zhì)P,并對其中具有性質(zhì)P的集合,寫出相應(yīng)的集合S和T;(2)
對任何具有性質(zhì)P的集合A,證明: ;
;
(3)
判斷m和n的大小關(guān)系,并證明你的結(jié)論.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(07年北京卷理)已知集合![]() ,其中
,其中![]() ,由
,由![]() 中的元素構(gòu)成兩個相應(yīng)的集合:
中的元素構(gòu)成兩個相應(yīng)的集合:
![]() ,
,![]() .
.
其中![]() 是有序數(shù)對,集合
是有序數(shù)對,集合![]() 和
和![]() 中的元素個數(shù)分別為
中的元素個數(shù)分別為![]() 和
和![]() .
.
若對于任意的![]() ,總有
,總有![]() ,則稱集合
,則稱集合![]() 具有性質(zhì)
具有性質(zhì)![]() .
.
(I)檢驗(yàn)集合![]() 與
與![]() 是否具有性質(zhì)
是否具有性質(zhì)![]() 并對其中具有性質(zhì)
并對其中具有性質(zhì)![]() 的集合,寫出相應(yīng)的集合
的集合,寫出相應(yīng)的集合![]() 和
和![]() ;
;
(II)對任何具有性質(zhì)![]() 的集合
的集合![]() ,證明:
,證明:![]() ;
;
(III)判斷![]() 和
和![]() 的大小關(guān)系,并證明你的結(jié)論.
的大小關(guān)系,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2007年普通高等學(xué)校招生全國統(tǒng)一考試?yán)砜茢?shù)學(xué)卷(北京) 題型:解答題
已知集合 ,其中
,其中 ,由
,由 中的元素構(gòu)成兩個相應(yīng)的集合:
中的元素構(gòu)成兩個相應(yīng)的集合: ,
, .其中
.其中 是有序數(shù)對,集合
是有序數(shù)對,集合 和
和 中的元素個數(shù)分別為
中的元素個數(shù)分別為 和
和 .若對于任意的
.若對于任意的 ,總有
,總有 ,則稱集合
,則稱集合 具有性質(zhì)
具有性質(zhì) .
.
(I)檢驗(yàn)集合 與
與 是否具有性質(zhì)
是否具有性質(zhì) 并對其中具有性質(zhì)
并對其中具有性質(zhì) 的集合,寫出相應(yīng)的集合
的集合,寫出相應(yīng)的集合 和
和 ;
;
(II)對任何具有性質(zhì) 的集合
的集合 ,證明:
,證明: ;
;
(III)判斷 和
和 的大小關(guān)系,并證明你的結(jié)論.
的大小關(guān)系,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
已知集合![]() ,其中
,其中![]() ,由
,由![]() 中的元素構(gòu)成兩個相應(yīng)的集合:
中的元素構(gòu)成兩個相應(yīng)的集合:
![]() ,
,![]() .
.
其中![]() 是有序數(shù)對,集合
是有序數(shù)對,集合![]() 和
和![]() 中的元素個數(shù)分別為
中的元素個數(shù)分別為![]() 和
和![]() .
.
若對于任意的![]() ,總有
,總有![]() ,則稱集合
,則稱集合![]() 具有性質(zhì)
具有性質(zhì)![]() .
.
(Ⅰ)檢驗(yàn)集合![]() 與
與![]() 是否具有性質(zhì)
是否具有性質(zhì)![]() 并對其中具有性質(zhì)
并對其中具有性質(zhì)![]() 的集合,寫出相應(yīng)的集合
的集合,寫出相應(yīng)的集合![]() 和
和![]() ;
;
(Ⅱ)對任何具有性質(zhì)![]() 的集合
的集合![]() ,證明:
,證明:![]() ;
;
(Ⅲ)判斷![]() 和
和![]() 的大小關(guān)系,并證明你的結(jié)論.
的大小關(guān)系,并證明你的結(jié)論.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com