
【題目】已知函數![]() .
.
(Ⅰ)若x軸為曲線![]() 的切線,求a的值;
的切線,求a的值;
(Ⅱ)求函數![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(Ⅰ)![]() (Ⅱ)詳見解析
(Ⅱ)詳見解析
【解析】
(Ⅰ)求出函數的導數,設切點坐標為(x0,0),求出切線的斜率,轉化求解即可;
(Ⅱ)求出f′(x)=3x2﹣a,通過當a≤0時,當a≥3時,當0<a<3時,判斷導函數的符號,判斷函數的單調性即可得到函數的最值.
解:(Ⅰ)由于x軸為![]() 的切線,設切點坐標為
的切線,設切點坐標為![]() ,則
,則![]() ,……①又
,……①又![]() ,即
,即![]() ,……②②代入①,解得
,……②②代入①,解得![]() ,
,
所以![]() .
.
(Ⅱ)![]() ,
,
(1)當![]() 時,
時,![]() ,
,![]() 在
在![]() 單調遞增,所以
單調遞增,所以![]() 時,
時,![]() 取得最小值
取得最小值![]() .
.
![]() 時,
時,![]() 取得最大值
取得最大值![]() .
.
(2)當![]() 時,
時,![]() ,
,![]() 在
在![]() 單調遞減,所以,
單調遞減,所以,![]() 時,
時,![]() 取得最小值
取得最小值![]() .
.
![]() 時,
時,![]() 取得最大值
取得最大值![]() .
.
(3).當![]() 時,令
時,令![]() ,解得
,解得![]() ,
,![]() ,
,![]() ,
,![]() 在區間
在區間![]() 的變化情況如下:
的變化情況如下:
|
|
|
|
|
| 0 |
|
| 單調遞減↗ | 極小值 | 單調遞增↘ |
由上表可知,當![]() 時,
時,![]() 取得最小值
取得最小值![]() ;
;
由于![]() ,
,![]() ,
,
當![]() 時,
時,![]() 在
在![]() 處取得最大值
處取得最大值![]() ,
,
當![]() 時,
時,![]() 在
在![]() 處取得最大值
處取得最大值![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在極坐標系![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,弧
,弧![]() ,
,![]() 所在圓的圓心分別是
所在圓的圓心分別是![]() ,
,![]() ,曲線
,曲線![]() 是弧
是弧![]() ,曲線
,曲線![]() 是線段
是線段![]() ,曲線
,曲線![]() 是線段
是線段![]() ,曲線
,曲線![]() 是弧
是弧![]() .
.
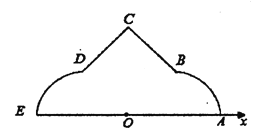
(1)分別寫出![]() ,
,![]() ,
,![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)曲線![]() 由
由![]() ,
,![]() ,
,![]() ,
,![]() 構成,若點
構成,若點![]() ,(
,(![]() ),在
),在![]() 上,則當
上,則當![]() 時,求點
時,求點![]() 的極坐標.
的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究“教學方式”對教學質量的影響,某高中數學老師分別用兩種不同的教學方式對入學數學平均分數和優秀率都相同的甲、乙兩個高一新班進行教學(勤奮程度和自覺性都一樣).以下莖葉圖為甲、乙兩班(每班均為20人)學生的數學期末考試成績.
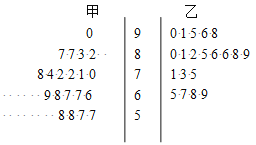
(1)學校規定:成績不低于75分的為優秀.請畫出下面的![]() 列聯表.
列聯表.
甲班 | 乙班 | 合計 | |
優秀 | |||
不優秀 | |||
合計 |
(2)判斷有多大把握認為“成績優秀與教學方式有關”.
下面臨界值表僅供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式: ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() ,直線
,直線![]() ,
,![]() 是
是![]() 圖象的任意兩條對稱軸,且
圖象的任意兩條對稱軸,且![]() 的最小值為
的最小值為![]() .
.
(1)求![]() 的表達式;
的表達式;
(2)將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位后,再將得到的圖象上各點的橫坐標伸長為原來的2倍,縱坐
個單位后,再將得到的圖象上各點的橫坐標伸長為原來的2倍,縱坐
標不變,得到函數![]() 的圖象,若關于
的圖象,若關于![]() 的方程
的方程![]() ,在區間
,在區間![]() 上有且只有一個實數解,求實數
上有且只有一個實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A、B兩種品牌各三種車型2017年7月的銷量環比(與2017年6月比較)增長率如下表:
A品牌車型 | A1 | A2 | A3 | ||||
環比增長率 | -7.29% | 10.47% | 14.70% | ||||
B品牌車型 | B1 | B2 | B3 | ||||
環比增長率 | -8.49% | -28.06% | 13.25% | ||||
根據此表中的數據,有如下關于7月份銷量的四個結論:①A1車型銷量比B1車型銷量多;
②A品牌三種車型總銷量環比增長率可能大于14.70%;
③B品牌三款車型總銷量環比增長率可能為正;
④A品牌三種車型總銷量環比增長率可能小于B品牌三種車型總銷量環比增長率.
其中正確結論的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A、B兩種品牌各三種車型2017年7月的銷量環比(與2017年6月比較)增長率如下表:
A品牌車型 | A1 | A2 | A3 | ||||
環比增長率 | -7.29% | 10.47% | 14.70% | ||||
B品牌車型 | B1 | B2 | B3 | ||||
環比增長率 | -8.49% | -28.06% | 13.25% | ||||
根據此表中的數據,有如下關于7月份銷量的四個結論:①A1車型銷量比B1車型銷量多;
②A品牌三種車型總銷量環比增長率可能大于14.70%;
③B品牌三款車型總銷量環比增長率可能為正;
④A品牌三種車型總銷量環比增長率可能小于B品牌三種車型總銷量環比增長率.
其中正確結論的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左頂點為
,左頂點為![]() ,過橢圓
,過橢圓![]() 的右焦點
的右焦點![]() 作互相垂直的兩條直線
作互相垂直的兩條直線![]() 分別交直線
分別交直線![]() 于
于![]() 兩點,
兩點,![]() 交橢圓
交橢圓![]() 于另一點
于另一點![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)求證:直線![]() 恒過定點,并求出定點坐標.
恒過定點,并求出定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2015年1月至2017年12月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.根據該折線圖,下列結論錯誤的是()
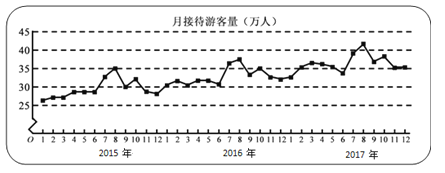
A. 年接待游客量逐年增加
B. 各年的月接待游客量高峰期在8月
C. 2015年1月至12月月接待游客量的中位數為30萬人
D. 各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一條直線上依次有三點![]() 、
、![]() 、
、![]() .一只獵犬在點
.一只獵犬在點![]() 發現一大兩小三只兔子從點
發現一大兩小三只兔子從點![]() 向兔穴(點
向兔穴(點![]() )前行,立即向它們追去.當兔子發現獵犬追趕后,急忙向兔穴奔跑,大兔為了提高速度,可叼著一只小兔奔跑(速度不變,且叼起與放下小兔所耽誤的時間不計).已知
)前行,立即向它們追去.當兔子發現獵犬追趕后,急忙向兔穴奔跑,大兔為了提高速度,可叼著一只小兔奔跑(速度不變,且叼起與放下小兔所耽誤的時間不計).已知![]() ,
,![]() ,獵犬、大兔、小兔奔跑的速度分別為
,獵犬、大兔、小兔奔跑的速度分別為![]() 、
、![]() 、
、![]() ,兔子前行的速度為
,兔子前行的速度為![]() .則三只兔子至多在離開點
.則三只兔子至多在離開點![]() ______
______![]() 時發現獵犬,才能恰在獵犬追上自己之前全部跑進兔穴.
時發現獵犬,才能恰在獵犬追上自己之前全部跑進兔穴.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com