
如圖一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。將△ABD沿邊AB折起, 使得△ABD與△ABC成30o的二面角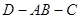 ,如圖二,在二面角
,如圖二,在二面角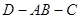 中.
中.
(1) 求CD與面ABC所成的角正弦值的大小;
(2) 對于AD上任意點H,CH是否與面ABD垂直。
(1)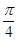
(2) CH不可能同時垂直BD和BA,即CH不與面ABD垂直
解析試題分析:解: 依題意,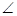 ABD=90o,建立如圖的坐標系使得△ABC在yoz平面上,
ABD=90o,建立如圖的坐標系使得△ABC在yoz平面上,
 △ABD與△ABC成30o的二面角,
△ABD與△ABC成30o的二面角, 
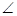 DBY=30o,又AB=BD=2,
DBY=30o,又AB=BD=2,  A(0,0,2),B(0,0,0),
A(0,0,2),B(0,0,0),
C(0, ,1),D(1,
,1),D(1, ,0),
,0),
(1) x軸與面ABC垂直,故(1,0,0)是面ABC的一個法向量。
x軸與面ABC垂直,故(1,0,0)是面ABC的一個法向量。
設CD與面ABC成的角為 ,而
,而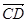 = (1,0,-1),
= (1,0,-1), sin
sin =
= =
=

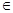 [0,
[0, ],
],
 =
=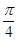 ; 6分
; 6分
(2) 設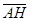 =t
=t = t(1,
= t(1, ,-2)= (t,
,-2)= (t, t,-2 t),
t,-2 t),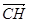 =
= +
+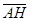 =(0,-
=(0,- ,1) +(t,
,1) +(t, t,-2 t) = (t,
t,-2 t) = (t, t-
t- ,-2 t+1),
,-2 t+1),
若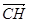
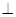
 ,則 (t,
,則 (t, t-
t- ,-2 t+1)·(0,0,2)="0" 得t=
,-2 t+1)·(0,0,2)="0" 得t= , 10分
, 10分
此時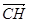 =(
=( ,-
,- ,0),而
,0),而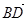 =(1,
=(1, ,0),
,0),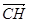 ·
·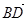 =
= -
- =-1
=-1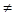 0,
0,
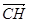 和
和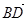 不垂直,即CH不可能同時垂直BD和BA,即CH不與面ABD垂直。 12分
不垂直,即CH不可能同時垂直BD和BA,即CH不與面ABD垂直。 12分
考點:空間中線面的位置關系
點評:主要是考查了空間中線面位置關系的運用,屬于基礎題。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:解答題
如圖已知:菱形 所在平面與直角梯形
所在平面與直角梯形 所在平面互相垂直,
所在平面互相垂直, ,
, 點
點 分別是線段
分別是線段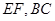 的中點.
的中點. 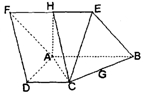
(1)求證:平面
 平面
平面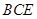 ;
;
(2)點 在直線
在直線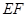 上,且
上,且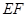 //平面
//平面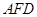 ,求平面
,求平面 與平面
與平面 所成角的余弦值。
所成角的余弦值。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,平面四邊形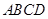 的4個頂點都在球
的4個頂點都在球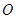 的表面上,
的表面上,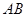 為球
為球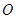 的直徑,
的直徑, 為球面上一點,且
為球面上一點,且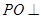 平面
平面 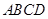 ,
,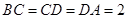 ,點
,點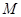 為
為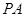 的中點.
的中點.
(1) 證明:平面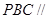 平面
平面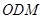 ;
;
(2) 求平面 與平面
與平面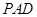 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。將△ABD沿邊AB折起, 使得△ABD與△ABC成30o的二面角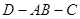 ,如圖二,在二面角
,如圖二,在二面角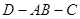 中.
中.
(1) 求CD與面ABC所成的角正弦值的大小;
(2) 對于AD上任意點H,CH是否與面ABD垂直。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,在四棱柱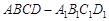 中,側棱
中,側棱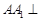 底面
底面 ,
,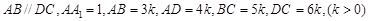
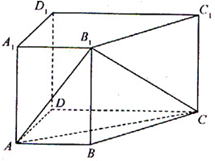
(Ⅰ)求證: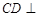 平面
平面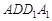
(Ⅱ)若直線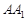 與平面
與平面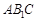 所成角的正弦值為
所成角的正弦值為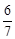 ,求
,求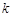 的值
的值
(Ⅲ)現(xiàn)將與四棱柱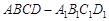 形狀和大小完全相同的兩個四棱柱拼成一個新的四棱柱,規(guī)定:若拼成的新四棱柱形狀和大小完全相同,則視為同一種拼接方案,問共有幾種不同的拼接方案?在這些拼接成的新四棱柱中,記其中最小的表面積為
形狀和大小完全相同的兩個四棱柱拼成一個新的四棱柱,規(guī)定:若拼成的新四棱柱形狀和大小完全相同,則視為同一種拼接方案,問共有幾種不同的拼接方案?在這些拼接成的新四棱柱中,記其中最小的表面積為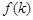 ,寫出
,寫出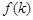 的解析式。(直接寫出答案,不必說明理由)
的解析式。(直接寫出答案,不必說明理由)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com