
(本小題滿分13分)
設a、b、c分別是先后擲一枚質地均勻的正方體骰子三次得到的點數.
(1)求使函數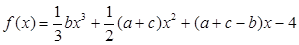 在R上不存在極值點的概率;
在R上不存在極值點的概率;
(2)設隨機變量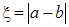 ,求
,求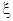 的分布列和數學期望.
的分布列和數學期望.
(1)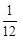 (2)
(2)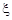 的分布列為
的分布列為
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
|
|
|
|
|
|
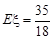
【解析】
試題分析:(1) ………………………………………(1分)
………………………………………(1分)
若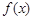 在R上不存在極值點,則
在R上不存在極值點,則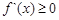 恒成立
恒成立
∴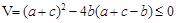 …………………………………………………………(2分)
…………………………………………………………(2分)
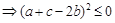
∴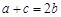
又a,b,c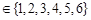
∴a、b、c成等差數列……………………………………………………………………(4分)
按公差分類,a、b、c成等差數列共有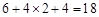 種情況
種情況
故函數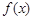 在R上不存在極值點的概率
在R上不存在極值點的概率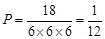 ……………………………(6分)
……………………………(6分)
(2)若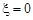 ,則
,則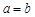 ∴
∴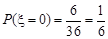
若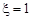 ,則
,則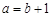 或
或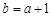 ,
,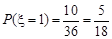
同理: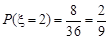
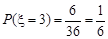
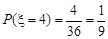
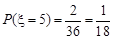 ……………………………………(10分)
……………………………………(10分)
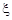 的分布列為
的分布列為
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
|
|
|
|
|
|
∴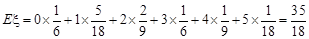 ………………………………(13分)
………………………………(13分)
考點:函數極值古典概率及分布列期望
點評:函數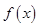 無極值點則導數
無極值點則導數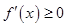 或
或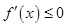 恒成立;古典概型概率需找到所有的基本事件總數及滿足題目要求的基本事件種數,求其比值;分布列首先找到隨機變量可取的值,然后結合題目背景依次求出各個概率
恒成立;古典概型概率需找到所有的基本事件總數及滿足題目要求的基本事件種數,求其比值;分布列首先找到隨機變量可取的值,然后結合題目背景依次求出各個概率


科目:高中數學 來源:2015屆江西省高一第二次月考數學試卷(解析版) 題型:解答題
(本小題滿分13分)已知函數
 .
.
(1)求函數 的最小正周期和最大值;
的最小正周期和最大值;
(2)在給出的直角坐標系中,畫出函數 在區間
在區間 上的圖象.
上的圖象.
(3)設0<x< ,且方程
,且方程 有兩個不同的實數根,求實數m的取值范圍.
有兩個不同的實數根,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高三年級八月份月考試卷理科數學 題型:解答題
(本小題滿分13分)已知定義域為 的函數
的函數 是奇函數.
是奇函數.
(1)求 的值;(2)判斷函數
的值;(2)判斷函數 的單調性;
的單調性;
(3)若對任意的 ,不等式恒成立
,不等式恒成立 ,求k的取值范圍.
,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源:河南省09-10學年高二下學期期末數學試題(理科) 題型:解答題
(本小題滿分13分)如圖,正三棱柱 的所有棱長都為2,
的所有棱長都為2, 為
為 的中點。
的中點。
(Ⅰ)求證: ∥平面
∥平面 ;
;
(Ⅱ)求異面直線 與
與 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

[來源:KS5
U.COM
查看答案和解析>>
科目:高中數學 來源:2010-2011學年福建省高三5月月考調理科數學 題型:解答題
(本小題滿分13分)
已知 為銳角,且
為銳角,且 ,函數
,函數 ,數列{
,數列{ }的首項
}的首項 .
.
(1) 求函數 的表達式;
的表達式;
(2)在 中,若
中,若 A=2
A=2 ,
, ,BC=2,求
,BC=2,求 的面積
的面積
(3) 求數列 的前
的前 項和
項和
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com