A市一卡車運送物資到相距120千米的B市,卡車每小時的費用L(元)可表示為車速v(千米/小時)平方的一次函數.當車速為60km/h時,每小時的費用為19元;當車速為90km/h時,每小時費用為31.5元.求:
(1)寫出每小時費用(L)與車速(v)之間的函數關系式;
(2)寫出本次運輸的總費用y(元)與車速v(km/h)的函數關系式并指出v為多大費用最省.(精確到1)
解:(1).由題意可設:L=kV
2+b
由已知中,當車速為60km/h時,每小時的費用為19元;
當車速為90km/h時,每小時費用為31.5元
代入得:19=k•60
2+b
31.5=k•90
2+b
解得:k=

,b=9
∴
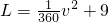
,v>0
(2)由(1)得y=L•t,t=
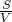
=
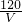
,
即
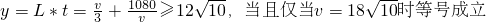
.
又∵18≈57
故速度為57km/h時郵費最省.
分析:(1)由已知中卡車每小時的費用L(元)可表示為車速v(千米/小時)平方的一次函數,故可可設:L=kV
2+b,由已知中車速為60km/h時,每小時的費用為19元;當車速為90km/h時,每小時費用為31.5元,我們可以構造參數k,b的方程,解方程求出參數的值,即可得到每小時費用(L)與車速(v)之間的函數關系式;
(2)由(1)中式子,結合時間t=
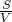
,我們可得總費用y(元)與車速v(km/h)的函數關系式,由基本不等式可以確定出費用最省時的車速.
點評:本題考查的知識點是函數模型的選擇與應用,基本不等式,待定系數法求函數的解析式,(1)的關鍵是由已知函數類型選擇待定系數法進行解答,(2)要注意題目中對結果精度度的要求,以免造成錯誤.

 ,b=9
,b=9 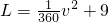 ,v>0
,v>0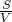 =
=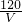 ,
,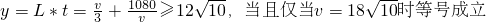 .
.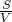 ,我們可得總費用y(元)與車速v(km/h)的函數關系式,由基本不等式可以確定出費用最省時的車速.
,我們可得總費用y(元)與車速v(km/h)的函數關系式,由基本不等式可以確定出費用最省時的車速.

 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案