
【題目】已知數列{an}的前n項和為Sn , 點(n, ![]() )在直線y=
)在直線y= ![]() x+
x+ ![]() 上. (Ⅰ)求數列{an}的通項公式;
上. (Ⅰ)求數列{an}的通項公式;
(Ⅱ)設bn= ![]() ,求數列{bn}的前n項和為Tn , 并求使不等式Tn>
,求數列{bn}的前n項和為Tn , 并求使不等式Tn> ![]() 對一切n∈N*都成立的最大正整數k的值.
對一切n∈N*都成立的最大正整數k的值.
【答案】解:(Ⅰ)由題意,得 ![]() =
= ![]() ,化為Sn=
,化為Sn= ![]() . 故當n≥2時,an=Sn﹣Sn﹣1=
. 故當n≥2時,an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() =n+5,
=n+5,
當n=1時,a1=S1=6=1+5,
∴an=n+5.
(Ⅱ)bn= ![]() =
= ![]() =
= ![]() ,
,
∴Tn= ![]() +…+
+…+ ![]()
= ![]() =
= ![]() .
.
由于Tn+1﹣Tn= ![]() =
= ![]() >0,
>0,
因此Tn單調遞增,
故(Tn)min=1.
令1 ![]() ,解得k<20,
,解得k<20,
∴kmax=19
【解析】(Ⅰ)由題意,得 ![]() =
= ![]() ,化為Sn=
,化為Sn= ![]() . 利用遞推關系即可得出.(2)利用“裂項求和”可得Tn , 再利用數列的單調性、不等式的性質即可得出.
. 利用遞推關系即可得出.(2)利用“裂項求和”可得Tn , 再利用數列的單調性、不等式的性質即可得出.
【考點精析】本題主要考查了數列的前n項和和數列的通項公式的相關知識點,需要掌握數列{an}的前n項和sn與通項an的關系 ;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式才能正確解答此題.
;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】四棱錐P﹣ABCD中,底面ABCD是邊長為2的菱形,側面PAD⊥底面ABCD,∠BCD=60°,PA=PD= ![]() ,E是BC中點,點Q在側棱PC上.
,E是BC中點,點Q在側棱PC上. 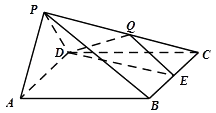
(1)求證:AD⊥PB;
(2)若Q是PC中點,求二面角E﹣DQ﹣C的余弦值;
(3)若 ![]() ,當PA∥平面DEQ時,求λ的值.
,當PA∥平面DEQ時,求λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() =1(a>b>0)過點(1,
=1(a>b>0)過點(1, ![]() ),左右焦點為F1、F2 , 右頂點為A,上頂點為B,且|AB|=
),左右焦點為F1、F2 , 右頂點為A,上頂點為B,且|AB|= ![]() |F1F2|.
|F1F2|.
(1)求橢圓E的方程;
(2)直線l:y=﹣x+m與橢圓E交于C、D兩點,與以F1、F2為直徑的圓交于M、N兩點,且 ![]() =
= ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有紅、黃、藍三種顏色小旗各2面,將他們排成3行2列,要求每行及每列的顏色均互不相同,則不同的排列方法共有( )
A. 12種 B. 18種 C. 24種 D. 36種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知c>0,設命題p:函數y=cx為減函數;命題q:當x∈[ ![]() ,2]時,函數f(x)=x+
,2]時,函數f(x)=x+ ![]() >
> ![]() 恒成立,如果p∨q為真命題,p∧q為假命題,求c的取值范圍.
恒成立,如果p∨q為真命題,p∧q為假命題,求c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖放置的邊長為1的正方形![]() 沿
沿![]() 軸滾動(向右為順時針,向左為逆時針).設頂點
軸滾動(向右為順時針,向左為逆時針).設頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則關于
,則關于![]() 的最小正周期
的最小正周期![]() 及
及![]() 在其兩個相鄰零點間的圖像與x軸所圍區域的面積S的正確結論是( )
在其兩個相鄰零點間的圖像與x軸所圍區域的面積S的正確結論是( )
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com