
【題目】在四棱錐中![]() 中,
中,![]() 是邊長為
是邊長為![]() 的等邊三角形,底面
的等邊三角形,底面![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
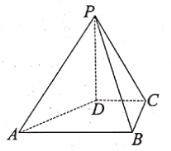
(1)證明:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,由
,由![]() 是等邊三角形可得
是等邊三角形可得![]() ,再由底面
,再由底面![]() 為直角梯形,結合已知的邊長可證得
為直角梯形,結合已知的邊長可證得![]() ,于是得
,于是得![]() 平面
平面![]() ,從而證得結果;
,從而證得結果;
(2)由條件可得可知![]() 兩兩垂直,所以以
兩兩垂直,所以以![]() 為坐標原點建立直角坐標系
為坐標原點建立直角坐標系![]() ,利用向量法求出二面角
,利用向量法求出二面角![]() 的余弦值.
的余弦值.
(1)證明:取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,因為
,因為![]() 是等邊三角形,所以
是等邊三角形,所以![]() .
.
因為在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,所以
,所以![]()
所以![]() 為等腰三角形,所以
為等腰三角形,所以![]()
因為![]() ,所以
,所以![]() 平面
平面![]()
因為![]() 平面
平面![]() ,所以
,所以![]() .
.
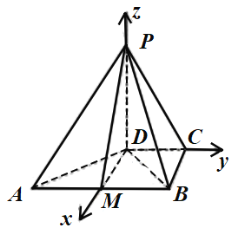
(2)解:因為![]() ,
,![]() ,
,![]() 為正三角形
為正三角形![]() 的
的![]() 邊上的高,所以
邊上的高,所以![]() .
.
因為![]() ,所以
,所以![]() ,由(1)可知
,由(1)可知![]() 兩兩垂直.
兩兩垂直.
以![]() 為坐標原點建立直角坐標系
為坐標原點建立直角坐標系![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]()
則![]() ,
,![]() ,
,![]()
設平面![]() 的法向量為
的法向量為![]()
則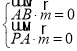 ,即
,即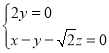 令
令![]() 得
得![]() .
.
設平面![]() 的法向量為
的法向量為![]()
則 ,即
,即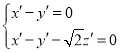 令
令![]() ,則
,則![]()
![]()
因為二面角![]() 為銳二面角,所以其余弦值為
為銳二面角,所以其余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】在脫貧攻堅中,某市教育局定點幫扶前進村![]() 戶貧困戶.駐村工作隊對這
戶貧困戶.駐村工作隊對這![]() 戶村民的貧困程度以及家庭平均受教育程度進行了調査,并將該村貧困戶按貧困程度分為“絕對貧困戶”與“相對貧困戶”,同時按家庭平均受教育程度分為“家庭平均受教育年限
戶村民的貧困程度以及家庭平均受教育程度進行了調査,并將該村貧困戶按貧困程度分為“絕對貧困戶”與“相對貧困戶”,同時按家庭平均受教育程度分為“家庭平均受教育年限![]() 年”與“家庭平均受教育年限
年”與“家庭平均受教育年限![]() 年”,具體調査結果如下表所示:
年”,具體調査結果如下表所示:
平均受教育年限 | 平均受教育年限 | 總計 | |
絕對貧困戶 | 10 | 40 | 50 |
相對貧困戶 | 20 | 30 | 50 |
總計 | 30 | 70 | 100 |
(1)為了參加扶貧辦公室舉辦的貧困戶“談心談話”活動,現通過分層抽樣從“家庭平均受教育年限![]() 年”的
年”的![]() 戶貧困戶中任意抽取
戶貧困戶中任意抽取![]() 戶,再從所抽取的
戶,再從所抽取的![]() 戶中隨機抽取
戶中隨機抽取![]() 戶參加“談心談話”活動,求至少有
戶參加“談心談話”活動,求至少有![]() 戶是絕對貧困戶的概率;
戶是絕對貧困戶的概率;
(2)根據上述表格判斷:是否有![]() 的把握認為貧困程度與家庭平均受教育程度有關?
的把握認為貧困程度與家庭平均受教育程度有關?
參考公式:![]()
參考數據:
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過橢圓![]() 的左頂點
的左頂點![]() 作斜率為2的直線,與橢圓的另一個交點為
作斜率為2的直線,與橢圓的另一個交點為![]() ,與
,與![]() 軸的交點為
軸的交點為![]() ,已知
,已知![]() .
.
(1)求橢圓的離心率;
(2)設動直線![]() 與橢圓有且只有一個公共點
與橢圓有且只有一個公共點![]() ,且與直線
,且與直線![]() 相交于點
相交于點![]() ,若
,若![]() 軸上存在一定點
軸上存在一定點![]() ,使得
,使得![]() ,求橢圓的方程.
,求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
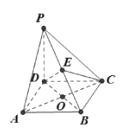
【題目】如圖,在四棱錐![]() 中,
中, ![]() 平面
平面![]() ,四邊形
,四邊形![]() 是菱形,
是菱形, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 交于點
交于點![]() ,
, ![]() 是
是![]() 上任意一點.
上任意一點.
(1)求證: ![]() ;
;
(2)已知二面角![]() 的余弦值為
的余弦值為![]() ,若
,若![]() 為
為![]() 的中點,求
的中點,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知真命題:“函數![]() 的圖象關于點
的圖象關于點![]() 成中心對稱圖形”的充要條件為“函數
成中心對稱圖形”的充要條件為“函數![]() 是奇函數”.
是奇函數”.
(Ⅰ)將函數![]() 的圖象向左平移1個單位,再向上平移2個單位,求此時圖象對應的函數解析式,并利用題設中的真命題求函數
的圖象向左平移1個單位,再向上平移2個單位,求此時圖象對應的函數解析式,并利用題設中的真命題求函數![]() 圖象對稱中心的坐標;
圖象對稱中心的坐標;
(Ⅱ)求函數![]() 圖象對稱中心的坐標;
圖象對稱中心的坐標;
(Ⅲ)已知命題:“函數![]() 的圖象關于某直線成軸對稱圖象”的充要條件為“存在實數
的圖象關于某直線成軸對稱圖象”的充要條件為“存在實數![]() 和
和![]() ,使得函數
,使得函數![]() 是偶函數”.判斷該命題的真假.如果是真命題,請給予證明;如果是假命題,請說明理由,并類比題設的真命題對它進行修改,使之成為真命題(不必證明).
是偶函數”.判斷該命題的真假.如果是真命題,請給予證明;如果是假命題,請說明理由,并類比題設的真命題對它進行修改,使之成為真命題(不必證明).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左頂點為
的左頂點為![]() ,右頂點為
,右頂點為![]() ,已知橢圓
,已知橢圓![]() 的離心率為
的離心率為![]() ,且以線段
,且以線段![]() 為直徑的圓被直線
為直徑的圓被直線![]() 所截的弦長為
所截的弦長為![]() .
.
(1)求橢圓的方程;
(2)記橢圓![]() 的右焦點為
的右焦點為![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線交橢圓于
的直線交橢圓于![]() 兩點.若線段
兩點.若線段![]() 的垂直平分線與
的垂直平分線與![]() 軸交于點
軸交于點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求f(x)的最大值;
(2)設函數![]() ,若對任意實數
,若對任意實數![]() ,當
,當![]() 時,函數
時,函數![]() 的最大值為
的最大值為![]() ,求a的取值范圍;
,求a的取值范圍;
(3)若數列![]() 的各項均為正數,
的各項均為正數,![]() ,
,![]() .求證:
.求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com