
【題目】設函數![]() .
.
(1)請作出該函數在長度為一個周期的閉區間的大致圖象;
(2)試判斷該函數的奇偶性,并運用函數的奇偶性定義說明理由;
(3)求該函數的單調遞增區間.
【答案】(1)見解析;(2)見解析;(3)![]() .
.
【解析】
(1)用五點法作圖,作出該函數在長度為一個周期的閉區間的大致圖象.(2)利用正弦函數的奇偶性作出判斷.(2)利用正弦函數的單調性,求函數單調遞增區間.
(1)函數f(x)=sin2x+cos2x=![]() sin(2x+
sin(2x+![]() ),
),
列表:
2x+ | 0 |
| π |
| 2π |
x | ﹣ |
|
|
|
|
f(x) | 0 |
| 0 | ﹣ | 0 |
作圖: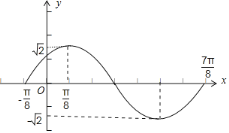
(2)該函數為非奇非偶,
∵f(﹣x)=![]() sin(﹣2x+
sin(﹣2x+![]() ),而f(x)=
),而f(x)=![]() sin(2x+
sin(2x+![]() ),
),
﹣f(x)=﹣![]() sin(2x+
sin(2x+![]() ),
),
∴f(﹣x)≠f(x),且f(x)≠﹣f(x),故f(x)為非奇非偶函數.
(3)令2kπ﹣![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]() ,求得kπ﹣
,求得kπ﹣![]() ≤x≤kπ+
≤x≤kπ+![]() ,
,
可得它的增區間為 ![]()


科目:高中數學 來源: 題型:
【題目】數列![]() 滿足:
滿足:![]() ,且
,且![]() ,其前n項和
,其前n項和![]() .
.
(1)求證:![]() 為等比數列;
為等比數列;
(2)記![]() 為數列
為數列![]() 的前n項和.
的前n項和.
(i)當![]() 時,求
時,求![]() ;
;
(ii)當![]() 時,是否存在正整數
時,是否存在正整數![]() ,使得對于任意正整數
,使得對于任意正整數![]() ,都有
,都有![]() ?如果存在,求出
?如果存在,求出![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,點E、F(E與A、D不重合)分別在棱AD,BD上,且EF⊥AD. 求證:(Ⅰ)EF∥平面ABC;
(Ⅱ)AD⊥AC.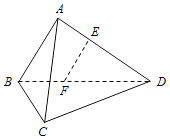
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,
,![]() .
.
(1)![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,函數
時,函數![]() 有兩個極值點,求
有兩個極值點,求![]() 的取值范圍;
的取值范圍;
(3)若![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸平行,且函數
軸平行,且函數![]() 在
在![]() 時,其圖象上每一點處切線的傾斜角均為銳角,求
時,其圖象上每一點處切線的傾斜角均為銳角,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() .
.
(1)請指出函數![]() 的定義域、周期性和奇偶性;(不必證明)
的定義域、周期性和奇偶性;(不必證明)
(2)請以正弦函數![]() 的性質為依據,并運用函數的單調性定義證明:
的性質為依據,并運用函數的單調性定義證明:![]() 在區間
在區間![]() 上單調遞減.
上單調遞減.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是樣本容量為200的頻率分布直方圖.根據樣本的頻率分布直方圖估計,樣本數落在[6,10]內的頻數為 ,數據落在(2,10)內的概率約為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 的前
的前![]() 項和為
項和為![]() ,若數列
,若數列![]() 的各項按如下規律排列:
的各項按如下規律排列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() , …,
, …,![]() ,…有如下運算和結論:①
,…有如下運算和結論:①![]() ;②數列
;②數列![]() ,
,![]() ,
,![]() ,
,![]() ,…是等比數列;③數列
,…是等比數列;③數列![]() ,
,![]() ,
,![]() ,
,![]() ,…的前
,…的前![]() 項和為
項和為![]() ;④若存在正整數
;④若存在正整數![]() ,使
,使![]() ,
,![]() ,則
,則![]() .其中正確的結論是_____.(將你認為正確的結論序號都填上)
.其中正確的結論是_____.(將你認為正確的結論序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=3,BC=2,點M,N分別是邊AB,CD上的點,且MN∥BC,![]()
![]() .若將矩形ABCD沿MN折起使其形成60°的二面角(如圖).
.若將矩形ABCD沿MN折起使其形成60°的二面角(如圖).

(1)求證:平面CND⊥平面AMND;
(2)求直線MC與平面AMND所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com