
(1)一個半徑為r的扇形,若它的周長等于弧所在的半圓的長,那么扇形的圓心角是多少弧度?是多少度?扇形的面積是多少?
(2)一扇形的周長為20 cm,當扇形的圓心角α等于多少弧度時,這個扇形的面積最大?
(1)π﹣2,65°26′, (π﹣2)r2.
(π﹣2)r2.
(2)當α=2rad時,扇形的面積取最大值.
【解析】
試題分析:(1)設(shè)扇形的圓心角,利用弧長公式得到弧長,代入題中條件,求出圓心角的弧度數(shù),再化為度數(shù),利用扇形的面積公式求扇形的面積.
(2)設(shè)出弧長和半徑,由周長得到弧長和半徑的關(guān)系,再把弧長和半徑的關(guān)系代入扇形的面積公式,轉(zhuǎn)化為關(guān)于半徑的二次函數(shù),配方求出面積的最大值.
【解析】
(1)設(shè)扇形的圓心角是θrad,因為扇形的弧長是rθ,
所以扇形的周長是2r+rθ.依題意,得2r+rθ=πr,
∴θ=π﹣2=(π﹣2)×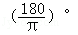 ≈1.142×57.30°≈65.44°≈65°26′,
≈1.142×57.30°≈65.44°≈65°26′,
∴扇形的面積為S= r2θ=
r2θ= (π﹣2)r2.
(π﹣2)r2.
(2)設(shè)扇形的半徑為r,弧長為l,則l+2r=20,
即l=20﹣2r(0<r<10)①
扇形的面積S= lr,將①代入,得S=
lr,將①代入,得S= (20﹣2r)r=﹣r2+10r=﹣(r﹣5)2+25,
(20﹣2r)r=﹣r2+10r=﹣(r﹣5)2+25,
所以當且僅當r=5時,S有最大值25.此時
l=20﹣2×5=10,α= =2.所以當α=2rad時,扇形的面積取最大值.
=2.所以當α=2rad時,扇形的面積取最大值.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源:[同步]2014年湘教版選修1-1 2.4 圓錐曲線的應(yīng)用練習(xí)卷(解析版) 題型:填空題
(5分)一個酒杯的軸截面是拋物線的一部分,它的方程是x2=2y(0≤y≤20).在杯內(nèi)放入一個玻璃球,要使球觸及酒杯底部,則玻璃球的半徑r的范圍為
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:[同步]2014年湘教版選修1-1 2.1 橢圓練習(xí)卷(解析版) 題型:選擇題
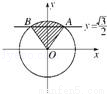
(3分)已知橢圓C的左、右焦點坐標分別是(﹣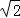 ,0),(
,0),(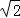 ,0),離心率是
,0),離心率是 ,則橢圓C的方程為( )
,則橢圓C的方程為( )
A.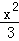 +y2=1 B.x2+
+y2=1 B.x2+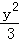 =1 C.
=1 C.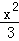 +y
+y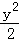 =1 D.
=1 D.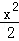 +
+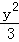 =1
=1
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:[同步]2014年湘教版必修二 3.1 弧度制與任意角練習(xí)卷2(解析版) 題型:解答題
(8分)1弧度的圓心角所對的弦長為2,求這個圓心角所對的弧長及圓心角所夾的扇形的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:[同步]2014年湘教版必修二 3.1 弧度制與任意角練習(xí)卷2(解析版) 題型:選擇題
(2分)將分針撥快10分鐘,則分針轉(zhuǎn)過的弧度數(shù)是( )
A.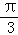 B.﹣
B.﹣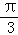 C.
C. D.﹣
D.﹣
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:[同步]2014年湘教版必修二 3.1 弧度制與任意角練習(xí)卷1(解析版) 題型:填空題
(5分)比較sin2,sin3與sin4的大小 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:[同步]2014年湘教版必修二 3.1 弧度制與任意角練習(xí)卷1(解析版) 題型:填空題
(5分)已知( )sin2θ<1,則θ所在象限為第 象限.
)sin2θ<1,則θ所在象限為第 象限.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:[同步]2014年湘教版必修三 7.5 空間直角坐標系練習(xí)卷(解析版) 題型:
在空間直角坐標系O﹣xyz中,z=1的所有點構(gòu)成的圖形是 .點P(2,3,5)到平面xOy的距離為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:[同步]2014年新人教B版選修4-5 2.3平均值不等式練習(xí)卷(解析版) 題型:選擇題
已知x,y,z∈R,且x+y+z=8,x2+y2+z2=24,則x的取值范圍是( )
A.[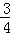 ,4] B.[
,4] B.[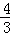 ,4] C.[
,4] C.[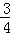 ,3] D.[
,3] D.[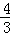 ,3]
,3]
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com