
���}Ŀ����֪�E�A![]() :
:![]() ��(j��ng)�^(gu��)�c(di��n)
��(j��ng)�^(gu��)�c(di��n)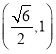 ���x���ʞ�
���x���ʞ�![]() .
.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���^(gu��)�c(di��n)![]() ��ֱ��
��ֱ��![]() ���E�A��
���E�A��![]() ��
��![]() ���c(di��n)��
���c(di��n)��![]() ��E�A
��E�A![]() �����c(di��n)����
�����c(di��n)����![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
���𰸡���1��![]() ����2��
����2��![]() ��
��![]()
��������
��1���əE�A���x���ʿɵ�![]() ��
��![]() ���Ķ�ʹ�E�A����ֻ��һ��(g��)δ֪��(sh��)
���Ķ�ʹ�E�A����ֻ��һ��(g��)δ֪��(sh��)![]() �����c(di��n)������(bi��o)���뷽�̺����
�����c(di��n)������(bi��o)���뷽�̺����![]() ���M(j��n)���õ��E�A�ķ��̞�
���M(j��n)���õ��E�A�ķ��̞�![]() ��
��
��2����?y��n)�ֱ���^(gu��)���c(di��n)![]() ������ֻҪ���ֱ����б�ʼ��ɣ��˕r(sh��)�茦(du��)ֱ����б�ʷֵ���0�Ͳ�����0�ɷN��r�M(j��n)��ӑՓ����(d��ng)б�ʲ���0�r(sh��)���O(sh��)ֱ��
������ֻҪ���ֱ����б�ʼ��ɣ��˕r(sh��)�茦(du��)ֱ����б�ʷֵ���0�Ͳ�����0�ɷN��r�M(j��n)��ӑՓ����(d��ng)б�ʲ���0�r(sh��)���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ���c(di��n)
���c(di��n)![]() ��
��![]() ������
������![]() �õ��P(gu��n)��
�õ��P(gu��n)��![]() �ķ��̣������
�ķ��̣������![]() .
.
��1���O(sh��)�E�A![]() �Ľ�����
�Ľ�����![]() ���t
���t![]() ��
��
��![]() ��
��![]() ��
��
���ԣ��E�A![]() �ķ��̞�
�ķ��̞�![]() ��
��
���c(di��n)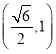 ������(bi��o)����E�A
������(bi��o)����E�A![]() �ķ��̵�
�ķ��̵�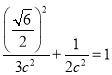 ��
��
���![]() ���t
���t![]() ��
��![]() ��
��
��ˣ��E�A![]() �ķ��̞�
�ķ��̞�![]() .
.
��2������(d��ng)ֱ��![]() б�ʞ�0�r(sh��)��
б�ʞ�0�r(sh��)��![]() �c�E�A����
�c�E�A����![]() ��
��![]() ����
����![]() .
.
�˕r(sh��)![]() ���ʲ������}��.
���ʲ������}��.
����(d��ng)ֱ��![]() б�ʲ���0�r(sh��)���O(sh��)ֱ��
б�ʲ���0�r(sh��)���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ���O(sh��)�c(di��n)
���O(sh��)�c(di��n)![]() ��
��![]() ��
��
��ֱ��![]() �ķ��̴���E�A�ķ��̣�������(ji��n)��
�ķ��̴���E�A�ķ��̣�������(ji��n)��![]() ��
��
![]() �����
�����![]() ��
��![]() ��
��
���f�_(d��)�����ɵ�![]() ��
��![]() ��
��
![]() ��ͬ���ɵ�
��ͬ���ɵ�![]() ��
��
����![]()
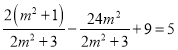 ����
����![]()
��ã�![]() �������}��
�������}��
��ˣ�ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() =Asin
=Asin![]() ��A>0��
��A>0��![]() >0��
>0��![]() <
<![]() ��
��![]() ����
����![]() ̎ȡ�����ֵ2����D���cx�S�������ɂ�(g��)���c(di��n)�ľ��x��
̎ȡ�����ֵ2����D���cx�S�������ɂ�(g��)���c(di��n)�ľ��x��![]() ��
��
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����(sh��)![]()
![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����˷�ӳ��(gu��)��(j��ng)��(j��)���ИI(y��)��(du��)�}(c��ng)��(ch��)�����I(y��)��(w��)������׃����r���Լ���Ҫ��Ʒ��(k��)��׃���Ą�(d��ng)���Ї�(gu��)�����c��ُ(g��u)(li��n)�ϕ�(hu��)���Ѓ�(ch��)�l(f��)չ�ɷ�����˾ͨ�^(gu��)(li��n)���{(di��o)�飬�ƶ����Ї�(gu��)�}(c��ng)��(ch��)ָ��(sh��)����D��ʾ���۾��D��2016��1����2017��12�µ��Ї�(gu��)�}(c��ng)��(ch��)ָ��(sh��)�߄�(sh��)��r��

����(j��)ԓ�۾��D�����нY(ji��)Փ���_����
A. 2016����µĂ}(c��ng)��(ch��)ָ��(sh��)���ֵ����3�·�
B. 2017��1����12�µĂ}(c��ng)��(ch��)ָ��(sh��)����λ��(sh��)��54%
C. 2017��1����4�µĂ}(c��ng)��(ch��)ָ��(sh��)��2016��ͬ�ڲ���(d��ng)�Ը���
D. 2017��11�µĂ}(c��ng)��(ch��)ָ��(sh��)�^�����������䣬�@ʾ���}(c��ng)��(ch��)�I(y��)��(w��)���(d��ng)��Ȼ�^����S����(j��ng)��(j��)�\(y��n)�з�(w��n)�����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() ���溯��(sh��)��e����Ȼ��(du��)��(sh��)�ĵה�(sh��)��.
���溯��(sh��)��e����Ȼ��(du��)��(sh��)�ĵה�(sh��)��.
��1����(sh��)��(sh��)a��ֵ��
��2����(sh��)![]() ��
��![]() �ϵ�ֵ��
�ϵ�ֵ��
��3����![]() ����ʽ
����ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�����
�У�����![]() �����Σ�
������![]() ��
��![]() �����c(di��n)��
�����c(di��n)��![]() ��
��![]() �����c(di��n)���C����ֱ��
�����c(di��n)���C����ֱ��![]() ƽ��
ƽ��![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() �������|(zh��)
�������|(zh��)![]() ����(du��)�����
����(du��)�����![]() ��
��![]() ��
��![]() ���c
���c![]() �ɔ�(sh��)��������һ��(g��)����
�ɔ�(sh��)��������һ��(g��)����![]() ��
��
��1���քe�Д���(sh��)��![]() �c
�c![]() �Ƿ�������|(zh��)
�Ƿ�������|(zh��)![]() �����f(shu��)�����ɣ�
�����f(shu��)�����ɣ�
��2���C����![]() ����
����![]() ��
��
��3����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����x��R�ϵĺ���(sh��)![]() �M��
�M��![]() ���Ү�(d��ng)
���Ү�(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ����(du��)����
����(du��)����![]() R������
R������![]() ��
��
��1�����C��![]() ��
��
��2�����C����(du��)����![]() R������
R������![]() ��
��
��3�����C��![]() ��R�ϵ�������(sh��)��
��R�ϵ�������(sh��)��
��4����![]() ����
����![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У�����C�ą���(sh��)���̞�
�У�����C�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S��ؓ(f��)���S��O�S�����O����(bi��o)ϵ.
�S��ؓ(f��)���S��O�S�����O����(bi��o)ϵ.
��1����������C�ĘO����(bi��o)���̣�
��2���O(sh��)�c(di��n)M�ĘO����(bi��o)��![]() ���^(gu��)�c(di��n)M��ֱ��
���^(gu��)�c(di��n)M��ֱ��![]() �c����C����A��B���c(di��n)����
�c����C����A��B���c(di��n)����![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��������(sh��)![]() �ڶ��x��
�ڶ��x��![]() ��(n��i)���{(di��o)�f������(sh��)��(sh��)
��(n��i)���{(di��o)�f������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��2����(du��)�����������(sh��)��(sh��)![]() ����
����![]() �����C��
�����C��![]() .
.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com