
���}Ŀ����ֱ������(bi��o)ϵ![]() �У�ֱ��
�У�ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)��
�酢��(sh��)��![]() ������ԭ�c(di��n)
������ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�������S��O�S�����O����(bi��o)ϵ������
�S�������S��O�S�����O����(bi��o)ϵ������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��1����ֱ��![]() �^�c(di��n)
�^�c(di��n)![]() ����ֱ��
����ֱ��![]() �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣�
��2����ֱ��![]() �c��������
�c��������![]() ���c(di��n)����
���c(di��n)����![]() �����ֵ.
�����ֵ.
���𰸡���1��![]() ��2��4
��2��4
����������������1����ֱ��![]() �^���c(di��n)
�^���c(di��n)![]() ����ֱ��
����ֱ��![]() �^�c(di��n)
�^�c(di��n)![]() �������
�������![]() ��ֱ��
��ֱ��![]() (
(![]() �酢��(sh��))����ȥ
�酢��(sh��))����ȥ![]() ����
����![]() ���ɴ˿���ֱ��
���ɴ˿���ֱ��![]() �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣�
��2������![]() ����ͨ���̞�
����ͨ���̞�![]() ��
��
��������![]() ����
����![]() ��A���ҽ�(j��ng)�^ԭ�c(di��n)�ĈA��
��A���ҽ�(j��ng)�^ԭ�c(di��n)�ĈA��
��?y��n)�ֱ��![]() �^�A��
�^�A��![]() ������
������![]() ������
������![]() ��
��
�ɴ˿���![]() �����ֵ.
�����ֵ.
Ԕ�⣺
��1����ֱ��![]() �^�c(di��n)
�^�c(di��n)![]() ��ע��
��ע��![]() ��
��
�Y(ji��)��![]() ����
����![]() ��
��
����ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�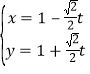 ��
��![]() �酢��(sh��)������ȥ
�酢��(sh��)������ȥ![]() ����
����![]() ��
��
��![]() ������
������![]() ��ֱ��
��ֱ��![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
��2������![]() ����ͨ���̞�
����ͨ���̞�![]() ��
��
��������![]() ����
����![]() ��A���ҽ�(j��ng)�^ԭ�c(di��n)�ĈA��
��A���ҽ�(j��ng)�^ԭ�c(di��n)�ĈA��
��?y��n)�ֱ��![]() �^�A��
�^�A��![]() ������
������![]() ������
������![]() ��
��
![]()
![]() ��
��
����![]() ����(d��ng)�҃H��(d��ng)
����(d��ng)�҃H��(d��ng)![]() �rȡ��̖����
�rȡ��̖����
��![]() �����ֵ��4..
�����ֵ��4..



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)�������О�![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����
���� ![]() ����
����![]() ��
�� ![]() ��
�� ![]() �������t��70����(sh��)���ǣ� ��
�������t��70����(sh��)���ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
(I)��(sh��)���c(di��n)(1��0)̎���о����̣�
(II)�O(sh��)��(sh��)��(sh��)kʹ��f(x)< kx���������k�ķ�����
(III)�O(sh��)����(sh��)![]() ����(sh��)h(x)�څ^(q��)�g
����(sh��)h(x)�څ^(q��)�g![]() �ϵ����c(di��n)����(sh��)��
�ϵ����c(di��n)����(sh��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
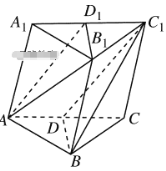
���}Ŀ����D��ʾ����б������ABC��A1B1C1�У��c(di��n)D��D1�քe��AC��A1C1�ϵ��c(di��n)��
(1)��(d��ng)![]() ��ֵ���ں�ֵ�r��BC1��ƽ��AB1D1��
��ֵ���ں�ֵ�r��BC1��ƽ��AB1D1��
(2)��ƽ��BC1D��ƽ��AB1D1����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij���S���a(ch��n)�a(ch��n)Ʒ![]() ���Ŀ��ɱ�
���Ŀ��ɱ�![]() ���fԪ��.��֪�a(ch��n)Ʒ�r
���fԪ��.��֪�a(ch��n)Ʒ�r![]() ���fԪ���c�a(ch��n)Ʒ����(sh��)
���fԪ���c�a(ch��n)Ʒ����(sh��)![]() �M��
�M��![]() �����a(ch��n)100���@�ӵĮa(ch��n)Ʒ�r��50�fԪ.
�����a(ch��n)100���@�ӵĮa(ch��n)Ʒ�r��50�fԪ.
��1���O(sh��)�a(ch��n)����![]() ���r����������
���r����������![]() ���fԪ������
���fԪ������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2���a(ch��n)��![]() ������ٕr������
������ٕr������![]() ���fԪ����������ֵ.
���fԪ����������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����Dl����������ABCD�У�AB=2��E��AB߅�����c(di��n)��F(xi��n)��BC߅�ϵ�һ�c(di��n)�����Ǿ�AC�քe��DE��DF��M��N���c(di��n)����ADAE��CDCF����ʹA��C�غ���A�c(di��n)����(g��u)����D2��ʾ�Ď��w��
��I�����C��A��D����A��EF��
����ԇ̽�����ڈD1�У�F(xi��n)��ʲôλ�Õr����ʹ�����Ď��w��EF��ƽ��AMN�����o���C����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ���L�S�L��4��ֱ��
���L�S�L��4��ֱ��![]() ���E�A
���E�A![]() �صõľ����L��
�صõľ����L��![]() .
.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���^�E�A![]() ������c(di��n)�����ഹֱ�ăɗlֱ��
������c(di��n)�����ഹֱ�ăɗlֱ��![]() �քe���E�A
�քe���E�A![]() ��
��![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() ��ͬ�ڙE�A
��ͬ�ڙE�A![]() ������c(di��n)�����C����ֱ��
������c(di��n)�����C����ֱ��![]() �^���c(di��n)
�^���c(di��n)![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����ABCD��߅AB=2��BC=1����A������(bi��o)ԭ�c(di��n)��AB��AD߅�քe��x�S��y�S�������S�ϣ�����ֱ������(bi��o)ϵ���������ۯB��ʹA�c(di��n)���ھ���DC�ϣ�����ӛ���c(di��n)![]()
(1)��(d��ng)�c(di��n)![]() ����(bi��o)��(1,1)�r�����ۺ�����ֱ������.
����(bi��o)��(1,1)�r�����ۺ�����ֱ������.
(2)���ۺ�����ֱ����б�ʞ�k��ԇ���ۺ�����ֱ���ķ��̣�
(3)��(d��ng)![]() �r���O(sh��)�ۺ�����ֱ���c
�r���O(sh��)�ۺ�����ֱ���c![]() �S�����c(di��n)E���c
�S�����c(di��n)E���c![]() �S�����c(di��n)F����
�S�����c(di��n)F����![]() ���ۺ�EF���D(zhu��n)��ʹ�����
���ۺ�EF���D(zhu��n)��ʹ�����![]() �Ĵ�С��
�Ĵ�С��![]() ���O(sh��)�����F
���O(sh��)�����F![]() ����������e��
����������e��![]() ��ԇ��
��ԇ��![]() ��Сֵ.
��Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��������(sh��)y=3sin��2x+ ![]() ���ĈD������ƽ��
���ĈD������ƽ�� ![]() ����λ�L�ȣ����ÈD��(y��ng)�ĺ���(sh��)�� ��
����λ�L�ȣ����ÈD��(y��ng)�ĺ���(sh��)�� ��
A.�څ^(q��)�g[ ![]() ��
�� ![]() ]�φ��{(di��o)�f�p
]�φ��{(di��o)�f�p
B.�څ^(q��)�g[ ![]() ��
�� ![]() ]�φ��{(di��o)�f��
]�φ��{(di��o)�f��
C.�څ^(q��)�g[�� ![]() ��
�� ![]() ]�φ��{(di��o)�f�p
]�φ��{(di��o)�f�p
D.�څ^(q��)�g[�� ![]() ��
�� ![]() ]�φ��{(di��o)�f��
]�φ��{(di��o)�f��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com