
【題目】設![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點.
的左、右焦點.
(1)若![]() 是該橢圓上的一個動點,求
是該橢圓上的一個動點,求![]() 的最大值和最小值;
的最大值和最小值;
(2)設過定點![]() 的直線
的直線![]() 與橢圓交于不同的兩點
與橢圓交于不同的兩點![]() ,且
,且![]() 為銳角(其中
為銳角(其中![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
【答案】(1)![]()
![]() ;(2)
;(2)![]() .
.
【解析】
(1)設出點P的坐標,向量坐標化得到![]() 的表達式,進而得到最值;(2)
的表達式,進而得到最值;(2)![]() 為銳角即
為銳角即![]() ,設出點AB的坐標,向量坐標化得到點積的表達式為:x1x2+y1y2,聯立直線和橢圓方程,由韋達定理得到結果.
,設出點AB的坐標,向量坐標化得到點積的表達式為:x1x2+y1y2,聯立直線和橢圓方程,由韋達定理得到結果.
(1)由已知得,F1(-![]() ,0),F2(
,0),F2(![]() ,0),設點P(x,y),
,0),設點P(x,y),
則![]() +y2=1,且-2≤x≤2.
+y2=1,且-2≤x≤2.
所以![]() ·
·![]() =(-
=(-![]() -x,-y)·(
-x,-y)·(![]() -x,-y)=x2-3+y2=x2-3+1-
-x,-y)=x2-3+y2=x2-3+1-![]() =
=![]() x2-2,
x2-2,
當x=0,即P(0,±1)時,(![]() ·
·![]() )min=-2;
)min=-2;
當x=±2,即P(±2,0)時,(![]() ·
·![]() )max=1.
)max=1.
(2)由題意可知,過點M(0,2)的直線l的斜率存在.
設l的方程為y=kx+2,
由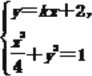 消去y,化簡整理得
消去y,化簡整理得
(1+4k2)x2+16kx+12=0,Δ=(16k)2-48(1+4k2)>0,解得k2>![]() .
.
設A(x1,y1),B(x2,y2),則x1+x2=-![]() ,x1x2=
,x1x2=![]() ,
,
又∠AOB為銳角,所以![]() ·
·![]() >0,即x1x2+y1y2>0,
>0,即x1x2+y1y2>0,
有x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4
=(1+k2)·![]() +2k·
+2k·![]() +4>0,解得k2<4,
+4>0,解得k2<4,
所以![]() <k2<4,即k∈
<k2<4,即k∈![]() .
.


科目:高中數學 來源: 題型:
【題目】[選修44:坐標系與參數方程]
在平面直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線
的直線![]() 的參數方程為
的參數方程為![]() (
(![]()
為參數).以坐標原點為極點,以![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標
的極坐標
方程是![]() .
.
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() .若點
.若點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 經過點
經過點![]() 且與曲線
且與曲線![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 兩點間的距離
兩點間的距離![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,拋物線
,拋物線![]() :
: ![]() 與拋物線
與拋物線![]() :
: ![]() 異于原點
異于原點![]() 的交點為
的交點為![]() ,且拋物線
,且拋物線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
(1)若直線![]() 與拋物線
與拋物線![]() 交于點
交于點![]() ,
, ![]() ,且
,且![]() ,求拋物線
,求拋物線![]() 的方程;
的方程;
(2)證明: ![]() 的面積與四邊形
的面積與四邊形![]() 的面積之比為定值.
的面積之比為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為
的定義域為![]() ,若存在常數
,若存在常數![]() ,使
,使![]() 對一切實數
對一切實數![]() 均成立,則稱
均成立,則稱![]() 為“倍約束函數”
為“倍約束函數”![]() 現給出下列函數:
現給出下列函數:![]() ;
;![]() ;
;![]() ;
;![]() 是定義在實數集
是定義在實數集![]() 上的奇函數,且對一切
上的奇函數,且對一切![]() ,
,![]() 均有
均有![]() 其中是“倍約束函數”的序號是
其中是“倍約束函數”的序號是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.

(I)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(II)若二面角P-CD-A的大小為45°,求直線PA與平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() 為參數),直線
為參數),直線![]() 經過點
經過點![]() ,且傾斜角為
,且傾斜角為![]() .
.
(1)寫出直線![]() 的參數方程和圓
的參數方程和圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,我國電子商務蓬勃發(fā)展,有關部門推出了針對網購平臺的商品和服務的評價系統,從該系統中隨機選出100次成功了的交易,并對這些交易的評價進行統計,網購者對商品的滿意率為0.6,對服務的滿意率為0.75,其中對商品和服務都滿意的交易為40次.
(1)根據已知條件完成下面的![]() 列聯表,并回答能否有
列聯表,并回答能否有![]() 的把握認為“網購者對服務滿意與對商品滿意之間有關”?
的把握認為“網購者對服務滿意與對商品滿意之間有關”?

(2)若將頻率視為概率,某人在該網購平臺上進行的3次購物中,設對商品和服務都滿意的次數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:  (其中
(其中![]() 為樣本容量)
為樣本容量)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網店統計了連續(xù)三天售出商品的種類情況:第一天售出19種商品,第二天售出13種商品,第三天售出18種商品;前兩天都售出的商品有3種,后兩天都售出的商品有4種,則該網店
①第一天售出但第二天未售出的商品有______種;
②這三天售出的商品最少有_______種.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節(jié)對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com