
【題目】如圖,在平面直角坐標系xOy中,橢圓C:![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,短軸長是2.
,短軸長是2.
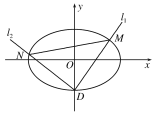
(1)求橢圓C的方程;
(2)設橢圓C的下頂點為D,過點D作兩條互相垂直的直線l1,l2,這兩條直線與橢圓C的另一個交點分別為M,N.設l1的斜率為k(k≠0),△DMN的面積為S,當![]() ,求k的取值范圍.
,求k的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由e=![]() ,2b=2,a2=b2+c2構造方程組,解出a,b即可得橢圓方程;(2)設l1的方程為y=kx-1代入橢圓方程,求出M的坐標,可得|DM|,用
,2b=2,a2=b2+c2構造方程組,解出a,b即可得橢圓方程;(2)設l1的方程為y=kx-1代入橢圓方程,求出M的坐標,可得|DM|,用![]() 代替k,可得|DN|,求出△DMN的面積S,可得
代替k,可得|DN|,求出△DMN的面積S,可得![]() ,解不等式
,解不等式![]() >
>![]() 可得k的取值范圍.
可得k的取值范圍.
(1)設橢圓C的半焦距為c,則由題意得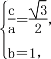 又a2=b2+c2,解得a=2,b=1,
又a2=b2+c2,解得a=2,b=1,
∴橢圓方程為![]() +y2=1.
+y2=1.
(2)由(1)知,橢圓C的方程為![]() +y2=1,
+y2=1,
所以橢圓C與y軸負半軸交點為D(0,-1).
因為l1的斜率存在,所以設l1的方程為y=kx-1.
代入![]() +y2=1,得M
+y2=1,得M![]() ,
,
從而|DM|=![]() =
=![]() .
.
用-![]() 代替k得|DN|=
代替k得|DN|=![]() .
.
所以△DMN的面積S=![]() ·
·![]() ×
×![]() =
=![]() .
.
則![]() =
=![]() ,
,
因為![]() >
>![]() ,即
,即![]() >
>![]() ,
,
整理得4k4-k2-14<0,解得-![]() <k2<2,
<k2<2,
所以0<k2<2,即-![]() <k<0或0<k<
<k<0或0<k<![]() .
.
從而k的取值范圍為(-![]() ,0)∪(0,
,0)∪(0,![]() ).
).


科目:高中數學 來源: 題型:
【題目】某大學畢業生參加一個公司的招聘考試,考試分筆試和面試兩個環節,筆試有![]() 、
、![]() 兩個題目,該學生答對
兩個題目,該學生答對![]() 、
、![]() 兩題的概率分別為
兩題的概率分別為![]() 、
、![]() ,兩題全部答對方可進入面試.面試要回答甲、乙兩個問題,該學生答對這兩個問題的概率均為
,兩題全部答對方可進入面試.面試要回答甲、乙兩個問題,該學生答對這兩個問題的概率均為![]() ,至少答對一個問題即可被聘用,若只答對一問聘為職員,答對兩問聘為助理(假設每個環節的每個題目或問題回答正確與否是相互獨立的).
,至少答對一個問題即可被聘用,若只答對一問聘為職員,答對兩問聘為助理(假設每個環節的每個題目或問題回答正確與否是相互獨立的).
(1)求該學生被公司聘用的概率;
(2)設該學生應聘結束后答對的題目或問題的總個數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() ),以橢圓內一點
),以橢圓內一點![]() 為中點作弦
為中點作弦![]() ,設線段
,設線段![]() 的中垂線與橢圓相交于
的中垂線與橢圓相交于![]() ,
, ![]() 兩點.
兩點.
(Ⅰ)求橢圓的離心率;
(Ⅱ)試判斷是否存在這樣的![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一個圓上,并說明理由.
在同一個圓上,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,正確命題的個數是( )
①若2b=a+c,則a,b,c成等差數列;
②“a,b,c成等比數列”的充要條件是“b2=ac”;
③若數列{an2}是等比數列,則數列{an}也是等比數列;
④若![]() ,則
,則![]()
A.3B.2C.1D.0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() 與向量
與向量![]() 的對應關系用
的對應關系用![]() 表示.
表示.
(1) 證明:對于任意向量![]() 、
、![]() 及常數m、n,恒有
及常數m、n,恒有![]() ;
;
(2) 證明:對于任意向量![]() ,
,![]() ;
;
(3) 證明:對于任意向量![]() 、
、![]() ,若
,若![]() ,則
,則![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中, 正確說法的個數是( )
①在用![]() 列聯表分析兩個分類變量
列聯表分析兩個分類變量![]() 與
與![]() 之間的關系時,隨機變量
之間的關系時,隨機變量![]() 的觀測值
的觀測值![]() 越大,說明“A與B有關系”的可信度越大
越大,說明“A與B有關系”的可信度越大
②以模型![]() 去擬合一組數據時,為了求出回歸方程,設
去擬合一組數據時,為了求出回歸方程,設![]() ,將其變換后得到線性方程
,將其變換后得到線性方程![]() ,則
,則![]() ,
,![]() 的值分別是
的值分別是![]() 和 0.3
和 0.3
③已知兩個變量具有線性相關關系,其回歸直線方程為![]() ,若
,若![]() ,
,![]() ,
,![]() ,則
,則![]()
A.0B.1C.2D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com