
設正整數數列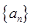 滿足:
滿足: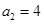 ,且對于任何
,且對于任何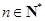 ,有
,有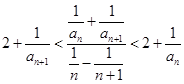 .
.
(1)求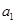 ,
,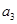 ;
;
(2)求數列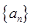 的通項
的通項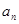 .
.
(1) 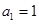 ,
,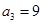 ;(2)
;(2) 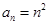 .
.
解析試題分析:(1)令 ,根據
,根據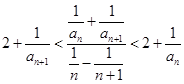 算得
算得 ,再根據
,再根據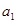 是正整數,算得.
是正整數,算得.
當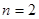 時,同樣根據
時,同樣根據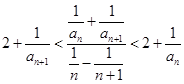 ,將
,將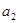 代入,得到
代入,得到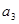 的范圍,根據
的范圍,根據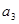 是正整數,求得
是正整數,求得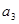 .
.
(2)先根據 可猜想
可猜想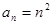 ,再用數學歸納法證明.
,再用數學歸納法證明.
試題解析:解:(1)據條件得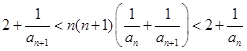 ①
①
當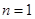 時,由
時,由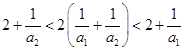 ,即有
,即有 ,
,
解得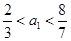 .因為
.因為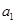 為正整數,故
為正整數,故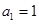 .
.
當 時,由
時,由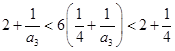 ,
,
解得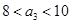 ,所以
,所以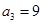 .
.
(2)方法一:由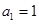 ,
,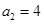 ,
,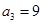 ,猜想:
,猜想: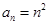 .
.
下面用數學歸納法證明.
1 當
當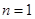 ,
,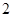 時,由(1)知
時,由(1)知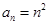 均成立;
均成立;
2 假設
假設 成立,則
成立,則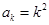 ,則
,則 時
時
由①得
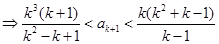
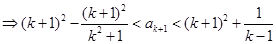
因為 時,
時, ,所以
,所以 .
. ,所以
,所以 .
.
又 ,所以
,所以 .
.
故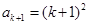 ,即
,即 時,
時,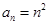 成立.
成立.
由1 ,2
,2 知,對任意
知,對任意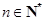 ,
,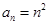 .
.
(2)方法二:
由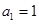 ,
,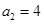 ,
,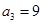 ,猜想:
,猜想: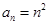 .
.
下面用數學歸納法證明.
1 當
當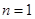 ,
,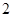 時,由(1)知
時,由(1)知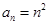 均成立;
均成立;
2 假設
假設 成立,則
成立,則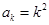 ,則
,則 時
時
由①得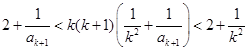
即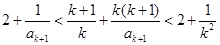 ②
②
由②左式,得 ,即
,即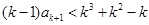 ,因為兩端為整數,
,因為兩端為整數,
則 .于是
.于是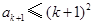 ③
③
又由②右式,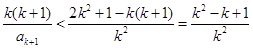 .
.
則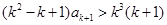 .
.
因為兩端為正整數,則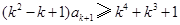 ,
,
所以

 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案科目:高中數學 來源: 題型:解答題
(14分)(2011•廣東)設b>0,數列{an}滿足a1=b,an=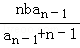 (n≥2)
(n≥2)
(1)求數列{an}的通項公式;
(2)證明:對于一切正整數n,2an≤bn+1+1.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設數列{an}的前n項和為Sn.已知a1=1,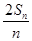 =an+1-
=an+1- n2-n-
n2-n-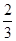 ,n∈N*.
,n∈N*.
(1)求a2的值;
(2)求數列{an}的通項公式;
(3)證明:對一切正整數n,有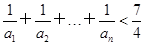 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com