
【題目】已知橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,橢圓
,橢圓![]() 過點(diǎn)
過點(diǎn) ,直線
,直線![]() 交
交![]() 軸于
軸于![]() ,且
,且![]() ,
,![]() 為坐標(biāo)原點(diǎn).
為坐標(biāo)原點(diǎn).
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() 是橢圓
是橢圓![]() 的上頂點(diǎn),過點(diǎn)
的上頂點(diǎn),過點(diǎn)![]() 分別作直線
分別作直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點(diǎn),設(shè)這兩條直線的斜率分別為
兩點(diǎn),設(shè)這兩條直線的斜率分別為![]() ,且
,且![]() ,證明:直線
,證明:直線![]() 過定點(diǎn).
過定點(diǎn).
【答案】(1)![]() ;(2)直線
;(2)直線![]() 過定點(diǎn)
過定點(diǎn)![]() .
.
【解析】
試題分析:(1)將點(diǎn) 代入橢圓方程得
代入橢圓方程得![]() ,由
,由![]() 得
得![]() ,則
,則![]() ,聯(lián)立方程得解;(2)分為直線
,聯(lián)立方程得解;(2)分為直線![]() 斜率存在和斜率不存在兩種情況,當(dāng)斜率不存在時,直接代入得解;當(dāng)斜率存在時,聯(lián)立直線和橢圓的方程得
斜率存在和斜率不存在兩種情況,當(dāng)斜率不存在時,直接代入得解;當(dāng)斜率存在時,聯(lián)立直線和橢圓的方程得![]() ,結(jié)合韋達(dá)定理,運(yùn)用整體代換的思想化簡得
,結(jié)合韋達(dá)定理,運(yùn)用整體代換的思想化簡得![]() ,可得其恒過定點(diǎn).
,可得其恒過定點(diǎn).
試題解析:(1)∵橢圓![]() 過點(diǎn)
過點(diǎn) ,∴
,∴![]() ① ,
① ,
∵![]() ,∴
,∴![]() ,則
,則![]() ,
,
∴![]() ②,由①②得
②,由①②得![]() ,
,
∴橢圓![]() 的方程為
的方程為![]()
(2)當(dāng)直線![]() 的斜率不存在時 ,設(shè)
的斜率不存在時 ,設(shè)![]() ,則
,則![]() ,由
,由![]() 得
得![]() ,得
,得![]()
當(dāng)直線![]() 的斜率存在時,設(shè)
的斜率存在時,設(shè)![]() 的方程為
的方程為![]() ,
,
 ,
,
得![]() ,
,
![]() ,
,
即![]() ,
,
由![]() ,
,
即![]() .
.
故直線![]() 過定點(diǎn)
過定點(diǎn)![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)△ABC的內(nèi)角A,B,C的對邊分別為a,b,c,若c=2![]() ,sinB=2sinA.
,sinB=2sinA.
(1)若C=![]() ,求a,b的值;
,求a,b的值;
(2)若cosC=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)有6名奧運(yùn)會志愿者,其中志愿者![]() 通曉日語,
通曉日語, ![]() 通曉俄語,
通曉俄語, ![]() 通曉韓語,從中選出通曉日語、俄語和韓語的志愿者各1名,組成一個小組.
通曉韓語,從中選出通曉日語、俄語和韓語的志愿者各1名,組成一個小組.
(1)求![]() 被選中的概率;
被選中的概率;
(2)求![]() 和
和![]() 不全被選中的概率;
不全被選中的概率;
(3)若6名奧運(yùn)會志愿者每小時派兩人值班,現(xiàn)有兩名只會日語的運(yùn)動員到來,求恰好遇到![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 外的有一點(diǎn)
外的有一點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作直線
作直線![]() .
.
(1)當(dāng)直線![]() 過圓心
過圓心![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(2)當(dāng)直線![]() 與圓
與圓![]() 相切時,求直線
相切時,求直線![]() 的方程;
的方程;
(3)當(dāng)直線![]() 的傾斜角為
的傾斜角為![]() 時,求直線
時,求直線![]() 被圓
被圓![]() 所截得的弦長.
所截得的弦長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() ,點(diǎn)
,點(diǎn)![]() 是直線
是直線![]() 上的一動點(diǎn),過點(diǎn)
上的一動點(diǎn),過點(diǎn)![]() 作圓
作圓![]() 的切線
的切線![]() ,切點(diǎn)為
,切點(diǎn)為![]() .
.
(1)當(dāng)切線![]() 的長度為
的長度為![]() 時,求點(diǎn)
時,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2) 若![]() 的外接圓為圓
的外接圓為圓![]() ,試問:當(dāng)
,試問:當(dāng)![]() 在直線
在直線![]() 上運(yùn)動時,圓
上運(yùn)動時,圓![]() 是否過定點(diǎn)?若存在,求出所有的定點(diǎn)的坐標(biāo);若不存在,說明理由.
是否過定點(diǎn)?若存在,求出所有的定點(diǎn)的坐標(biāo);若不存在,說明理由.
(3)求線段![]() 長度的最小值.
長度的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某玩具生產(chǎn)公司每天計劃生產(chǎn)衛(wèi)兵、騎兵、傘兵這三種玩具共100個,生產(chǎn)一個衛(wèi)兵需5分鐘,生產(chǎn)一個騎兵需7分鐘,生產(chǎn)一個傘兵需4分鐘,已知總生產(chǎn)時間不超過10小時,若生產(chǎn)一個衛(wèi)兵可獲利潤5元,生產(chǎn)一個騎兵可獲利潤6元,生產(chǎn)一個傘兵可獲利潤3元.
(1)用每天生產(chǎn)的衛(wèi)兵個數(shù)![]() 與騎兵個數(shù)
與騎兵個數(shù)![]() 表示每天的利潤
表示每天的利潤![]() (元);
(元);
(2)怎樣分配生產(chǎn)任務(wù)才能使每天的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)是否存在實(shí)數(shù)![]() ,使函數(shù)
,使函數(shù)![]() 在
在![]() 上有最小值2?若存在,求出
上有最小值2?若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《九章算術(shù)》中,將底面為長方形且有一條側(cè)棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.如圖,網(wǎng)格紙上正方形小格的邊長為1,圖中粗線畫出的是某幾何體毛坯的三視圖,第一次切削,將該毛坯得到一個表面積最大的長方體;第二次切削沿長方體的對角面刨開,得到兩個三棱柱;第三次切削將兩個三棱柱分別沿棱和表面的對角線刨開得到兩個鱉臑和兩個陽馬,則陽馬與鱉臑的體積之比為( )
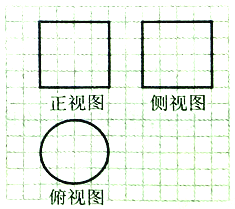
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)不等式組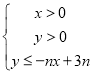 所表示的平面區(qū)域為Dn,記Dn內(nèi)的格點(diǎn)(格點(diǎn)即橫坐標(biāo)和縱坐標(biāo)均為整數(shù)的點(diǎn))的個數(shù)為f(n)(n∈N*).
所表示的平面區(qū)域為Dn,記Dn內(nèi)的格點(diǎn)(格點(diǎn)即橫坐標(biāo)和縱坐標(biāo)均為整數(shù)的點(diǎn))的個數(shù)為f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表達(dá)式;
(2)設(shè)bn=2nf(n),Sn為{bn}的前n項和,求Sn;
(3)記![]() ,若對于一切正整數(shù)n,總有Tn≤m成立,求實(shí)數(shù)m的取值范圍.
,若對于一切正整數(shù)n,總有Tn≤m成立,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com