【題目】已知函數
，
.
（1）討論
極值點的個數；
（2）若
，不等式
恒成立，當
為正數時，求
的最小值.
【答案】（1）
時，
在
上沒有極值點.當
時，在上有兩個極值點； （2）
.
【解析】
（1）求導可得
，可知導函數的最小值為
，當
時，
恒成立，沒有極值點，當
時，
，由于
，只需要討論二次方程
的解得情況即可；（2）不等式
恒成立，即
恒成立，構造函數
，對其求導，求出它的最小值為
，即
，然后結合基本不等式即可求出
的最小值。
（1），
時，恒成立，
在上是增函數，沒有極值點.
當時，，
二次方程中，
，
，
，
二次方程有兩個不等的正根.
在上有兩個根，在上有兩個極值點.
綜上所述，時，在上沒有極值點.當時，在上有兩個極值點.
（2）不等式恒成立，即恒成立.
記，
，
時，
，
，
在上是增函數，
時，
，
，在上是減函數，
，
當
為正數時，
，
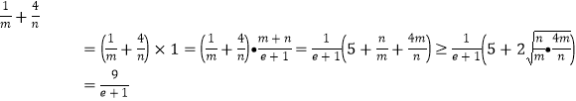當且僅當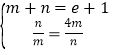
即
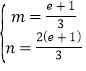時取等號.
的最小值為.
周周清檢測系列答案
輕巧奪冠周測月考直通高考系列答案科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足a1＝1， 
，其中n∈N*．
（1）設
，求證：數列{bn}是等差數列，并求出{an}的通項公式．
（2）設
，數列{cncn+2}的前n項和為Tn，是否存在正整數m，使得
對于n∈N*，恒成立？若存在，求出m的最小值；若不存在，請說明．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近年來，共享單車已經悄然進入了廣大市民的日常生活，并慢慢改變了人們的出行方式.為了更好地服務民眾，某共享單車公司在其官方
中設置了用戶評價反饋系統，以了解用戶對車輛狀況和優惠活動的評價.現從評價系統中選出
條較為詳細的評價信息進行統計，車輛狀況的優惠活動評價的
列聯表如下：
對優惠活動好評 | 對優惠活動不滿意 | 合計 | |
對車輛狀況好評 |
|
|
|
對車輛狀況不滿意 |
|
|
|
合計 |
|
|
|
（1）能否在犯錯誤的概率不超過
的前提下認為優惠活動好評與車輛狀況好評之間有關系？
（2）為了回饋用戶，公司通過向用戶隨機派送騎行券.用戶可以將騎行券用于騎行付費，也可以通過轉贈給好友.某用戶共獲得了
張騎行券，其中只有
張是一元券.現該用戶從這張騎行券中隨機選取張轉贈給好友，求選取的張中至少有
張是一元券的概率.
參考數據：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式：
，其中
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系，將曲線
上的每一個點的橫坐標保持不變，縱坐標縮短為原來的
，得到曲線
，以坐標原點
為極點， 
軸的正半軸為極軸，建立極坐標系， 
的極坐標方程為
．
（Ⅰ）求曲線
的參數方程；
（Ⅱ）過原點
且關于
軸對稱的兩條直線
與
分別交曲線
于
、
和
、
，且點
在第一象限，當四邊形
的周長最大時，求直線
的普通方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1，一個正四棱柱形的密閉容器底部鑲嵌了同底的正四棱錐形實心裝飾塊，容器內盛有
升水時，水面恰好經過正四棱錐的頂點P．如果將容器倒置，水面也恰好過點
（圖2）．有下列四個命題：
A．正四棱錐的高等于正四棱柱高的一半 |
B．將容器側面水平放置時，水面也恰好過點 |
C．任意擺放該容器，當水面靜止時，水面都恰好經過點 |
D．若往容器內再注入 |
其中真命題的代號是： （寫出所有真命題的代號）．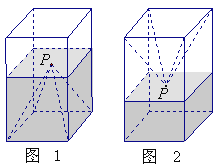
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】四色猜想是世界三大數學猜想之一，1976年數學家阿佩爾與哈肯證明，稱為四色定理.其內容是：“任意一張平面地圖只用四種顏色就能使具有共同邊界的國家涂上不同的顏色.”用數學語言表示為“將平面任意地細分為不相重疊的區域，每一個區域總可以用
，
，
，
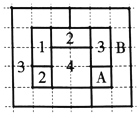
四個數字之一標記，而不會使相鄰的兩個區域得到相同的數字.”如圖，網格紙上小正方形的邊長為，粗實線圍城的各區域上分別標有數字，，，的四色地圖符合四色定理，區域
和區域
標記的數字丟失.若在該四色地圖上隨機取一點，則恰好取在標記為的區域的概率所有可能值中，最大的是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著新高考改革的不斷深入，高中學生生涯規劃越來越受到社會的關注.一些高中已經開始嘗試開設學生生涯規劃選修課程，并取得了一定的成果.下表為某高中為了調查學生成績與選修生涯規劃課程的關系，隨機抽取50名學生的統計數據.
成績優秀 | 成績不夠優秀 | 總計 | |
選修生涯規劃課 | 15 | 10 | 25 |
不選修生涯規劃課 | 6 | 19 | 25 |
總計 | 21 | 29 | 50 |
（Ⅰ）根據列聯表運用獨立性檢驗的思想方法能否有
的把握認為“學生的成績是否優秀與選修生涯規劃課有關”，并說明理由；
（Ⅱ）如果從全校選修生涯規劃課的學生中隨機地抽取3名學生，求抽到成績不夠優秀的學生人數
的分布列和數學期望（將頻率當作概率計算）.
參考附表：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
參考公式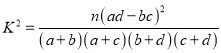
，其中
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
