
【題目】已知圓C:x2+y2﹣2x+4my+4m2=0,圓C1:x2+y2=25,以及直線l:3x﹣4y﹣15=0.
(1)求圓C1:x2+y2=25被直線l截得的弦長;
(2)當m為何值時,圓C與圓C1的公共弦平行于直線l;
(3)是否存在m,使得圓C被直線l所截的弦AB中點到點P(2,0)距離等于弦AB長度的一半?若存在,求圓C的方程;若不存在,請說明理由.
【答案】解:(1)因為圓![]() 的圓心O(0,0),半徑r=5,
的圓心O(0,0),半徑r=5,
所以,圓心O到直線l:3x﹣4y﹣15=0的距離d:![]() ,由勾股定理可知,
,由勾股定理可知,
圓![]() 被直線l截得的弦長為
被直線l截得的弦長為![]() .
.
(2)圓C與圓C1的公共弦方程為2x﹣4my﹣4m2﹣25=0,
因為該公共弦平行于直線3x﹣4y﹣15=0,
則![]() ≠
≠![]() ,
,
解得:m=![]()
經檢驗m=![]() 符合題意,故所求m=
符合題意,故所求m=![]() ;
;
(3)假設這樣實數m存在.
設弦AB中點為M,由已知得|AB|=2|PM|,即|AM|=|BM|=|PM|
所以點P(2,0)在以弦AB為直徑的圓上.
設以弦AB為直徑的圓方程為:x2+y2﹣2x+4my+4m2+λ(3x﹣4y﹣15)=0,
則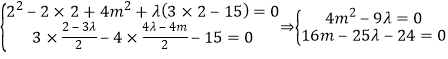
消去λ得:100m2﹣144m+216=0,25m2﹣36m+54=0
因為△=362﹣4×25×54=36(36﹣25×6)<0
所以方程25m2﹣36m+54=0無實數根,
所以,假設不成立,即這樣的圓不存在.
【解析】(1)根據直線和圓相交的弦長公式即可求圓C1:x2+y2=25被直線l截得的弦長;
(2)求出兩圓的公共弦結合直線平行的條件即可求出直線l;
(3)根據兩點間的距離公式結合弦長關系即可得到結論.


科目:高中數學 來源: 題型:
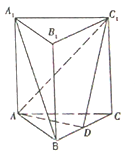
【題目】如圖,三棱柱![]() 中,底面
中,底面![]() 為正三角形,
為正三角形, ![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中點.
的中點.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)在側棱![]() 上是否存在一點
上是否存在一點![]() ,使得三棱錐
,使得三棱錐![]() 的體積是
的體積是![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,說明理由.
的長;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一條生產線上按同樣的方式每隔30分鐘取一件產品,共取了n件,測得其產品尺寸后,畫得其頻率分布直方圖如圖所示,已知尺寸在[15,45)內的頻數為46. 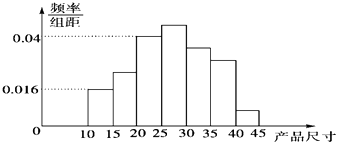
(1)該抽樣方法是什么方法?
(2)求n的值;
(3)求尺寸在[20,25)內的產品的件數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市出租車的計價標準是:4km以內(含4km)10元,超過4km且不超過18km的部分1.2元/km,超過18km的部分1.8元/km,不計等待時間的費用.
(1)如果某人乘車行駛了10km,他要付多少車費?
(2)試建立車費y(元)與行車里程x(km)的函數關系式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ),
),![]() 為
為![]() 上一點,以
上一點,以![]() 為邊作等邊三角形
為邊作等邊三角形![]() ,且
,且![]() 、
、![]() 、
、![]() 三點按逆時針方向排列.
三點按逆時針方向排列.
(Ⅰ)當點![]() 在
在![]() 上運動時,求點
上運動時,求點![]() 運動軌跡的直角坐標方程;
運動軌跡的直角坐標方程;
(Ⅱ)若曲線![]() :
: ![]() ,經過伸縮變換
,經過伸縮變換![]() 得到曲線
得到曲線![]() ,試判斷點
,試判斷點![]() 的軌跡與曲線
的軌跡與曲線![]() 是否有交點,如果有,請求出交點的直角坐標,沒有則說明理由.
是否有交點,如果有,請求出交點的直角坐標,沒有則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
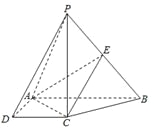
【題目】如圖,在四棱錐![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點.
的中點.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值為
的余弦值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com