
【題目】設函數![]() ,
,![]() .
.
(1)若曲線![]() 與曲線
與曲線![]() 在它們的交點
在它們的交點![]() 處具有公共切線,求a,b的值;
處具有公共切線,求a,b的值;
(2)當![]() 時,若函數
時,若函數![]() 在區間
在區間![]() 內恰有兩個零點,求a的取值范圍;
內恰有兩個零點,求a的取值范圍;
(3)![]() ,求函數
,求函數![]() 在區間
在區間![]() 上的最小值.
上的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)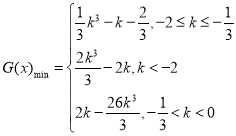
【解析】
(1)由題意求出![]() 由題意得
由題意得![]() ,且
,且![]() 解該方程組即可求出
解該方程組即可求出![]() 的值;(2)把
的值;(2)把![]() 代入
代入![]() 化簡,并求出
化簡,并求出![]() ,利用導數求出單調性和極值,由函數在
,利用導數求出單調性和極值,由函數在![]() 內有兩零點列出不等式組,求出不等式的解集可得
內有兩零點列出不等式組,求出不等式的解集可得![]() 的取值范圍.
的取值范圍.
(3)表示出![]() ,并求出
,并求出![]() ,利用導數求出單調性和極值點,按照在區間
,利用導數求出單調性和極值點,按照在區間![]() 內沒有極值點,一個極值點,兩個極值點分類討論,結合圖象及函數的單調性即可求得其最小值.
內沒有極值點,一個極值點,兩個極值點分類討論,結合圖象及函數的單調性即可求得其最小值.
(1)![]() ,
,![]() ,
,
![]() 由線
由線![]() 與曲線
與曲線![]() 在它們的交點
在它們的交點![]() 處具有公共切線,
處具有公共切線,
![]() ,
,![]() ,
,
即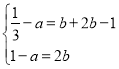 ,
,
解得![]() .
.
(2)![]() ,
,
![]() ,
,
![]()
![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,
,
|
|
|
|
|
|
| |
|
| 極小值 |
|
![]() 在
在![]() 內恰有2個零點,
內恰有2個零點,
 ,即
,即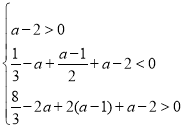 ,
,
解得![]() ,
,
因此a的取值范圍是![]() .
.
(3)![]()
![]()
![]()
![]()
令![]() ,解得
,解得![]() ,
,
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
| 極大值 |
| 極小值 |
|
①當![]() ,即
,即![]() 時,
時,![]() ,
,
![]() 在
在![]() 和
和![]() 單調遞增,
單調遞增,
![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() ,
,
![]()
![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,![]() .
.
②![]() ,即
,即![]() ,
,
![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() .
.
③![]() ,即
,即![]() ,
,
![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() 在
在![]() 單調遞增,
單調遞增,
![]() .
.
綜上所述,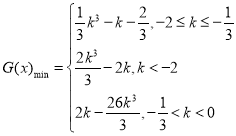 .
.


科目:高中數學 來源: 題型:
【題目】直線![]() ax+by=1與圓x2+y2=1相交于A,B兩點(其中a,b是實數),且△AOB是直角三角形(O是坐標原點),則點P(a,b)與點(0,1)之間距離的最小值為( ).
ax+by=1與圓x2+y2=1相交于A,B兩點(其中a,b是實數),且△AOB是直角三角形(O是坐標原點),則點P(a,b)與點(0,1)之間距離的最小值為( ).
A.0B.![]() C.
C.![]() -1D.
-1D.![]() +1
+1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學根據學生的興趣愛好,分別創建了“書法”、“詩詞”、“理學”三個社團,據資料統計新生通過考核選拔進入這三個社團成功與否相互獨立.2015年某新生入學,假設他通過考核選拔進入該校的“書法”、“詩詞”、“理學”三個社團的概率依次為![]() 、
、![]() 、
、![]() ,己知三個社團他都能進入的概率為
,己知三個社團他都能進入的概率為![]() ,至少進入一個社團的概率為
,至少進入一個社團的概率為![]() ,且
,且![]() .
.
(1)求![]() 與
與![]() 的值;
的值;
(2)該校根據三個社團活動安排情況,對進入“書法”社的同學增加校本選修學分1分,對進入“詩詞”社的同學增加校本選修學分2分,對進入“理學”社的同學增加校本選修學分3分.求該新同學在社團方面獲得校本選修課學分分數不低于4分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 ,其中
,其中![]() 為參數,
為參數,![]() .在以坐標原點
.在以坐標原點![]() 為極點,軸的正半軸為極軸的極坐標系中,點
為極點,軸的正半軸為極軸的極坐標系中,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的直角坐標方程與曲線
的直角坐標方程與曲線![]() 的普通方程;
的普通方程;
(2)若![]() 是曲線
是曲線![]() 上的動點,
上的動點,![]() 為線段
為線段![]() 的中點.求點
的中點.求點![]() 到直線
到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數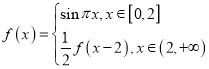 ,有下列說法:
,有下列說法:
①函數![]() 對任意
對任意![]() ,都有
,都有![]() 成立;
成立;
②函數![]() 在
在![]() 上單調遞減;
上單調遞減;
③函數![]() 在
在![]() 上有3個零點;
上有3個零點;
④若函數![]() 的值域為
的值域為![]() ,設
,設![]() 是
是![]() 中所有有理數的集合,若簡分數
中所有有理數的集合,若簡分數![]() (其中
(其中![]() ,
,![]() 為互質的整數),定義函數
為互質的整數),定義函數![]() ,則
,則![]() 在
在![]() 中根的個數為5;
中根的個數為5;
其中正確的序號是______(填寫所有正確結論的番號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠家舉行大型的促銷活動,經測算某產品當促銷費用為![]() 萬元時,銷售量
萬元時,銷售量![]() 萬件滿足
萬件滿足![]() (其中
(其中![]() ,
, ![]() 為正常數),現假定生產量與銷售量相等,已知生產該產品
為正常數),現假定生產量與銷售量相等,已知生產該產品![]() 萬件還需投入成本
萬件還需投入成本![]() 萬元(不含促銷費用),產品的銷售價格定為
萬元(不含促銷費用),產品的銷售價格定為![]() 萬元/萬件.
萬元/萬件.
(1)將該產品的利潤![]() 萬元表示為促銷費用
萬元表示為促銷費用![]() 萬元的函數;
萬元的函數;
(2)促銷費用投入多少萬元時,廠家的利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2013年華人數學家張益唐證明了孿生素數猜想的一個弱化形式。孿生素數猜想是希爾伯特在1900年提出的23個問題之一,可以這樣描述:存在無窮多個素數p,使得p+2是素數,素數對(p,p+2)稱為孿生素數.在不超過30的素數中,隨機選取兩個不同的數,其中能夠組成孿生素數的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,四邊形
中,四邊形![]() 為梯形,
為梯形, ![]() ,且
,且![]() ,
, ![]() 是邊長為2的正三角形,頂點
是邊長為2的正三角形,頂點![]() 在
在![]() 上的射影為點
上的射影為點![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.
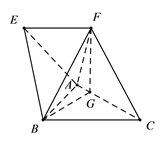
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com