
 為坐標原點,點
為坐標原點,點 的坐標為
的坐標為 ,點
,點 的坐標為
的坐標為 ,其中
,其中 且
且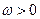 .設
.設 .
. ,
, ,
, ,求方程
,求方程 在區間
在區間 內的解集;
內的解集; 是曲線
是曲線 上的動點.當
上的動點.當 時,設函數
時,設函數 的值域為集合
的值域為集合 ,不等式
,不等式 的解集為集合
的解集為集合 . 若
. 若 恒成立,求實數
恒成立,求實數 的最大值;
的最大值; 的性質取決于變量
的性質取決于變量 、
、 和
和 的值. 當
的值. 當 時,試寫出一個條件,使得函數
時,試寫出一個條件,使得函數 滿足“圖像關于點
滿足“圖像關于點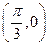 對稱,且在
對稱,且在 處
處 取得最小值”.【說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.】
取得最小值”.【說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.】 在
在 內的解集為
內的解集為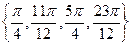
 的最大值
的最大值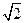 .
.  滿足“圖像關于點
滿足“圖像關于點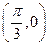 對稱,且在
對稱,且在 處
處 取得最小值”的充要條件是“當
取得最小值”的充要條件是“當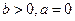 時,
時,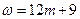 (
(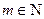 )或當
)或當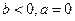 時,
時,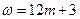 (
(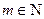 )”.
)”.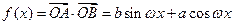 ,…………………………1分
,…………………………1分 ,
, ,
, 時,
時,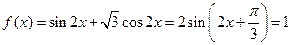 ,…2分
,…2分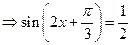 ,則有
,則有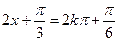 或
或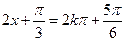 ,
,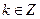 .
.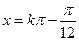 或
或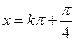 ,
,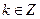 . ……………4分
. ……………4分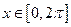 ,故
,故 在
在 內的解集為
內的解集為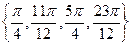 .……5分
.……5分 是曲線
是曲線 上的動點,故
上的動點,故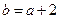 . ……………6分
. ……………6分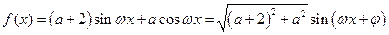 ,
, 的值域
的值域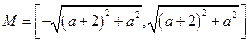 . ……………8分
. ……………8分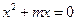 的解為0和
的解為0和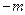 ,故要使
,故要使 恒成立,只需
恒成立,只需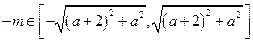 ,而
,而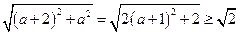 ,
,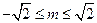 ,所以
,所以 的最大值
的最大值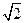 . …………………10分
. …………………10分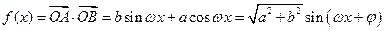 ,
,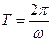 .
. 須滿足“圖像關于點
須滿足“圖像關于點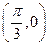 對稱,且在
對稱,且在 處
處 取得最小值”.
取得最小值”.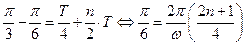
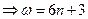 ,
,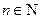 .
.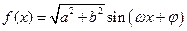 的函數的圖像的對稱中心都是
的函數的圖像的對稱中心都是 的零點,故需滿足
的零點,故需滿足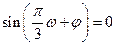 ,而當
,而當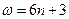 ,
,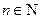 時,
時,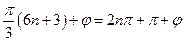 ,
,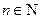 ;所以當且僅當
;所以當且僅當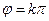 ,
,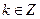 時,
時, 的圖像關于點
的圖像關于點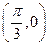 對稱;此時,
對稱;此時,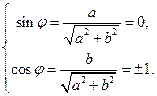
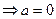 ,
,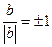 .
.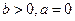 時,
時,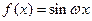 ,進一步要使
,進一步要使 處
處 取得最小值,則有
取得最小值,則有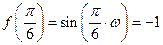
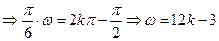 ,
,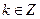 ;又
;又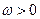 ,則有
,則有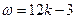 ,
,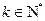 ;因此,由
;因此,由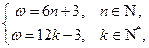 可得
可得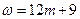 ,
,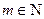 ;
;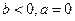 時,
時,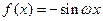 ,進一步要使
,進一步要使 處
處 取得最小值,則有
取得最小值,則有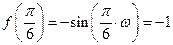
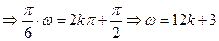 ,
,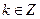 ;又
;又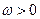 ,則有
,則有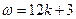 ,
,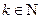 ;因此,由
;因此,由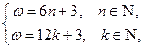 可得
可得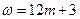 ,
,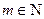 ;
; 滿足“圖像關于點
滿足“圖像關于點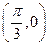 對稱,且在
對稱,且在 處
處 取得最小值”的充要條件是“當
取得最小值”的充要條件是“當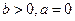 時,
時,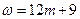 (
(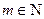 )或當
)或當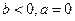 時,
時,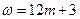 (
(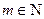 )”. ……………………………………………………14分
)”. ……………………………………………………14分

 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:高中數學 來源:不詳 題型:解答題
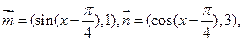
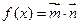 。
。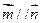 ,求
,求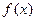 ;
;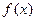 的圖像向右平移
的圖像向右平移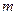 (
(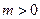 )個單位長度,再向下平移3個單位后圖像對應的函數
)個單位長度,再向下平移3個單位后圖像對應的函數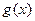 是奇函數,求
是奇函數,求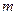 的最大值。
的最大值。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com