【題目】從4名男生和2名女生中任選3人參加演講比賽，設隨機變量ξ表示所選3人中女生的人數．
（1）求所選3人中女生人數ξ≤1的概率；
（2）求ξ的分布列及數學期望．
科目：高中數學 來源： 題型：
【題目】設全集U=R，集合A={x|1≤x＜4}，B={x|2a≤x＜3-a}．
（1）若a=-2，求B∩A，B∩(UA)；（2）若A∪B=A，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，圓
為圓
上任意一點，過
作圓的切線，分別交直線
和
于
兩點，連接
，相交于點
，若點的軌跡為曲線
.
（1）設直線的斜率分別為
，求
的值，并求曲線的方程；
（2）記直線
與曲線有兩個不同的交點
，與直線交于點
，與直線
交于點
，求
的面積與
的面積的比值
的最大值及取得最大值時
的值.
（注：
在點
處的切線方程為
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】據統計一次性飲酒4.8兩誘發腦血管病的概率為0.04，一次性飲酒7.2兩誘發腦血管病的概率為0.16.已知某公司職員一次性飲酒4.8兩未誘發腦血管病，則他還能繼續飲酒2.4兩不誘發腦血管病的概率為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從全校參加數學競賽的學生的試卷中抽取一個樣本，考察競賽的成績分布情況，將樣本分成5組，繪成頻率分布直方圖，圖中從左到右各小長方形的高之比為
，最右邊一組頻數是6，請結合直方圖提供的信息，解答下列問題：
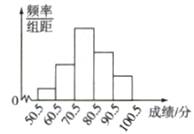
（1）樣本量是多少？
（2）列出頻率分布表.
（3）估計這次競賽中，成績高于60分的學生占總人數的百分比.
（4）成績落在哪個范圍內的人數最多？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在底面是菱形的四棱錐
中, 
平面
， 
，點
分別為
的中點，設直線
與平面
交于點
.
（1）已知平面
平面
，求證： 
.
（2）求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】物聯網（Internet of Things，縮寫：IOT）是基于互聯網、傳統電信網等信息承載體，讓所有能行使獨立功能的普通物體實現互聯互通的網絡. 其應用領域主要包括運輸和物流、工業制造、健康醫療、智能環境（家庭、辦公、工廠）等，具有十分廣闊的市場前景. 現有一家物流公司計劃租地建造倉庫儲存貨物，經過市場調查了解到下列信息：倉庫每月土地占地費
（單位：萬元），倉庫到車站的距離
（單位：千米，
），其中與
成反比，每月庫存貨物費
（單位：萬元）與成正比;若在距離車站9千米處建倉庫，則和分別為2萬元和7. 2萬元. 這家公司應該把倉庫建在距離車站多少千米處，才能使兩項費用之和最小？最小費用是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數f1（x），f2（x），h（x），如果存在實數a，b使得h（x）=af1（x）+bf2（x），那么稱h（x）為f1（x），f2（x）的生成函數.
（1）函數f1（x）=x2﹣x，f2（x）=x2+x+1，h（x）=x2﹣x+1，h（x）是否為f1（x），f2（x）的生成函數？說明理由；
（2）設f1（x）=1﹣x，f2（x）=
，當a=b=1時生成函數h（x），求h（x）的對稱中心（不必證明）；
（3）設f1（x）=x，
（x≥2），取a=2，b＞0，生成函數h（x），若函數h（x）的最小值是5，求實數b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
