
【題目】 (1)已知正數a,b滿足a+b=1,求證:a2+b2≥![]() ;
;
(2)設a、b、c為△ABC的三條邊,求證:a2+b2+c2<2(ab+bc+ca).
【答案】(1)見解析(2)見解析
【解析】
試題(1)利用配方將a2+b2化為1-2ab,再根據基本不等式證不等式(2)根據三角形兩邊之和大于第三邊得a+c>b,即得ab+bc>b2,同理可得bc+ca>c2 ,ab+ca>a2,三式相加即得結論
試題解析:證明:(1)a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =1-
=1-![]() =
=![]() .
.
(2)因為a,b,c是△ABC的三邊,不妨設a≥b≥c>0,則a>b-c≥0,b>a-c≥0,c>a-b≥0.平方得:
a2>b2+c2-2bc,b2>a2+c2-2ac,c2>a2+b2-2ab,
三式相加得:0>a2+b2+c2-2bc-2ac-2ab.
所以2ab+2bc+2ac>a2+b2+c2,
即a2+b2+c2<2(ab+bc+ca).


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
【題目】已知全集為R,函數f(x)=lg(1﹣x)的定義域為集合A,集合B={x|x2﹣x﹣6>0}.
(Ⅰ)求A∪B;
(Ⅱ)若C={x|m﹣1<x<m+1},C(A∩(RB)),求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知從![]() 地去
地去![]() 地有①或②兩條路可走,并且汽車走路①堵車的概率為
地有①或②兩條路可走,并且汽車走路①堵車的概率為![]() ,汽車走路②堵車的概率為
,汽車走路②堵車的概率為![]() ,若現在有兩輛汽車走路①,有一輛汽車走路②,且這三輛車是否堵車相互之間沒有影響,
,若現在有兩輛汽車走路①,有一輛汽車走路②,且這三輛車是否堵車相互之間沒有影響,
(1)若這三輛汽車中恰有一輛汽車被堵的概率為![]() ,求走路②堵車的概率;
,求走路②堵車的概率;
(2)在(1)的條件下,求這三輛汽車中被堵車輛的輛數![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列![]() 和等比數列
和等比數列![]() ,其中
,其中![]() 的公差不為0.設
的公差不為0.設![]() 是數列
是數列![]() 的前n項和.若
的前n項和.若![]() ,
,![]() ,
,![]() 是數列
是數列![]() 的前3項,且
的前3項,且![]() .
.
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)若數列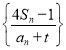 為等差數列,求實數t;
為等差數列,求實數t;
(3)構造數列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,….若該數列前n項和
,….若該數列前n項和![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品,每售出一噸可獲利![]() 萬元,每積壓一噸則虧損
萬元,每積壓一噸則虧損![]() 萬元.某經銷商統計出過去
萬元.某經銷商統計出過去![]() 年里市場年需求量的頻數分布表如下表所示.
年里市場年需求量的頻數分布表如下表所示.
年需求量(噸) |
|
|
|
|
|
年數 |
|
|
|
|
|
(1)求過去![]() 年年需求量的平均值;(每個區間的年需求量用中間值代替)
年年需求量的平均值;(每個區間的年需求量用中間值代替)
(2)今年該經銷商欲進貨![]() 噸,以
噸,以![]() (單位:噸,
(單位:噸,![]() )表示今年的年需求量,以
)表示今年的年需求量,以![]() (單位:萬元)表示今年銷售的利潤,試將
(單位:萬元)表示今年銷售的利潤,試將![]() 表示
表示![]() 的函數解析式,并求今年的年利潤不少于
的函數解析式,并求今年的年利潤不少于![]() 萬元的概率.
萬元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)的定義域為(-2,2),函數g(x)=f(x-1)+f(3-2x).
(1)求函數g(x)的定義域;
(2)若f(x)是奇函數,且在定義域上單調遞減,求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() ,
, ![]() ,則下列說法正確的是( )
,則下列說法正確的是( )
A. 把![]() 上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移
上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
B. 把![]() 上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移
上各點橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
C. 把曲線![]() 向右平移
向右平移![]() 個單位長度,再把得到的曲線上各點橫坐標縮短到原來的
個單位長度,再把得到的曲線上各點橫坐標縮短到原來的![]() ,縱坐標不變,得到曲線
,縱坐標不變,得到曲線![]()
D. 把曲線![]() 向右平移
向右平移![]() 個單位長度,再把得到的曲線上各點橫坐標縮短到原來的
個單位長度,再把得到的曲線上各點橫坐標縮短到原來的![]() ,縱坐標不變,得到曲線
,縱坐標不變,得到曲線![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com