
【題目】一位網(wǎng)民在網(wǎng)上光顧某網(wǎng)店,經(jīng)過一番瀏覽后,對該店鋪中的A,B,C三種商品有購買意向.已知該網(wǎng)民購買A種商品的概率為 ![]() ,購買B種商品的槪率為
,購買B種商品的槪率為 ![]() ,購買C種商品的概率為
,購買C種商品的概率為 ![]() .假設該網(wǎng)民是否購買這三種商品相互獨立
.假設該網(wǎng)民是否購買這三種商品相互獨立
(1)求該網(wǎng)民至少購買2種商品的概率;
(2)用隨機變量η表示該網(wǎng)民購買商品的種數(shù),求η的槪率分布和數(shù)學期望.
【答案】
(1)解:記“記網(wǎng)民購買i種商品”為事件Ai,i=2,3,
則P(A3)= ![]() ,
,
P(A2)= ![]() +
+ ![]() =
= ![]() ,
,
∴該網(wǎng)民至少購買2種商品的概率:
p=p(A1)+P(A2)= ![]() =
= ![]()
(2)解:隨機變量η的可能取值為0,1,2,3,
P(η=0)=(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )=
)= ![]() ,
,
P(η=2)=P(A2)= ![]() ,
,
P(η=3)=P(A3)= ![]() ,
,
∴P(η=1)=1﹣ ![]() =
= ![]() ,
,
∴隨機變量η的分布列為:
η | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eη= ![]() =
= ![]()
【解析】(1)記“記網(wǎng)民購買i種商品”為事件Ai , i=2,3,分別求出P(A3)和P(A2),由此能求出該網(wǎng)民至少購買2種商品的概率.(2)隨機變量η的可能取值為0,1,2,3,分別求出相應的概率,由此能求出隨機變量η的分布列和Eη.
【考點精析】解答此題的關鍵在于理解離散型隨機變量及其分布列的相關知識,掌握在射擊、產(chǎn)品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列.


科目:高中數(shù)學 來源: 題型:
【題目】已知某公司生產(chǎn)某產(chǎn)品的年固定成本為100萬元,每生產(chǎn)1千件需另投入27萬元,設該公司一年內生產(chǎn)該產(chǎn)品![]() 千件
千件![]() 并全部銷售完,每千件的銷售收入為
并全部銷售完,每千件的銷售收入為![]() 萬元,且
萬元,且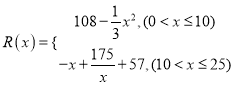 .
.
⑴ 寫出年利潤![]() (萬元)關于年產(chǎn)量
(萬元)關于年產(chǎn)量![]() (千件)的函數(shù)解析式;
(千件)的函數(shù)解析式;
⑵ 當年產(chǎn)量為多少千件時,該公司在這一產(chǎn)品的生產(chǎn)中所獲年利潤最大?(注:年利潤=年銷售收入![]() 年總成本).
年總成本).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設f(x)、g(x)分別是定義在R上的奇函數(shù)和偶函數(shù),當x<0時,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,則不等式f(x)g(x)<0的解集是( )
A.(﹣3,0)∪(3,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(3,+∞)
D.(﹣∞,﹣3)∪(0,3)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】將函數(shù)y=sin2x的圖象向左平移 ![]() 個單位長度,所得函數(shù)是( )
個單位長度,所得函數(shù)是( )
A.奇函數(shù)
B.偶函數(shù)
C.既是奇函數(shù)又是偶函數(shù)
D.既不是奇函數(shù)也不是偶函數(shù)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在某次水下科研考察活動中,需要潛水員潛入水深為60米的水底進行作業(yè),根據(jù)以往經(jīng)驗,潛水員下潛的平均速度為![]() (米/單位時間),每單位時間的用氧量為
(米/單位時間),每單位時間的用氧量為![]() (升),在水底作業(yè)10個單位時間,每單位時間用氧量為0.9(升),返回水面的平均速度為
(升),在水底作業(yè)10個單位時間,每單位時間用氧量為0.9(升),返回水面的平均速度為![]() (米/單位時間),每單位時間用氧量為1.5(升),記該潛水員在此次考察活動中的總用氧量為
(米/單位時間),每單位時間用氧量為1.5(升),記該潛水員在此次考察活動中的總用氧量為![]() (升).
(升).
(1)求![]() 關于
關于![]() 的函數(shù)關系式;
的函數(shù)關系式;
(2)若![]() ,求當下潛速度
,求當下潛速度![]() 取什么值時,總用氧量最少.
取什么值時,總用氧量最少.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓 ![]() 的左、右焦點分別為F1、F2 , 短軸兩個端點為A、B,且四邊形F1AF2B是邊長為2的正方形.
的左、右焦點分別為F1、F2 , 短軸兩個端點為A、B,且四邊形F1AF2B是邊長為2的正方形. 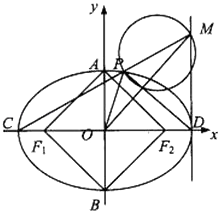
(1)求橢圓的方程;
(2)若C、D分別是橢圓長的左、右端點,動點M滿足MD⊥CD,連接CM,交橢圓于點P.證明: ![]() 為定值.
為定值.
(3)在(2)的條件下,試問x軸上是否存異于點C的定點Q,使得以MP為直徑的圓恒過直線DP、MQ的交點,若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知集合A={x|3≤3x≤27}, ![]() .
.
(1)分別求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求實數(shù)a的取值集合.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知f(x)=4sinωxsin(ωx+ ![]() )﹣1(ω>0),f(x)的最小正周期為π. (Ⅰ)當x∈[0,
)﹣1(ω>0),f(x)的最小正周期為π. (Ⅰ)當x∈[0, ![]() ]時,求f(x)的最大值;
]時,求f(x)的最大值;
(Ⅱ)請用“五點作圖法”畫出f(x)在[0,π]上的圖象.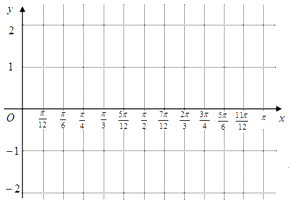
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com