
【題目】設![]() 是圓
是圓![]() 上的一動點,點
上的一動點,點![]() 在直線
在直線![]() 上線段
上線段![]() 的垂直平分線交直線
的垂直平分線交直線![]() 于點
于點![]() .
.
(1)若點![]() 的軌跡為橢圓,則求
的軌跡為橢圓,則求![]() 的取值范圍;
的取值范圍;
(2)設![]() 時對應的橢圓為
時對應的橢圓為![]() ,
,![]() 為橢圓的右頂點,直線
為橢圓的右頂點,直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() ,求
,求![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由已知可得點![]() 在
在![]() 的垂直平分線上,有
的垂直平分線上,有![]() ,進而
,進而![]() ,根據點
,根據點![]() 的軌跡為橢圓,由橢圓定義可得
的軌跡為橢圓,由橢圓定義可得![]() ,即
,即![]() 在圓
在圓![]() 外,得出
外,得出![]() 不等量關系,結合
不等量關系,結合![]() 關系,即可求解;
關系,即可求解;
(2)根據(1)求出橢圓方程,設出直線![]() ,以及
,以及![]() ,
,![]() ,根據直線與橢圓相交關系結合韋達定理,求出
,根據直線與橢圓相交關系結合韋達定理,求出![]() 的值,
的值,![]() 轉坐標關系,可得出直線
轉坐標關系,可得出直線![]() 過定點
過定點![]() ,得到
,得到![]() ,再利用韋達定理,求出
,再利用韋達定理,求出![]() 關于
關于![]() 的目標函數,結合
的目標函數,結合![]() 的范圍,利用換元法,轉化為二次函數的最值,即可求解.
的范圍,利用換元法,轉化為二次函數的最值,即可求解.
解:(1)若![]() 的軌跡為橢圓,則
的軌跡為橢圓,則![]() 必在圓內,
必在圓內,
此時![]() 的垂直平分線交線段
的垂直平分線交線段![]() 于點
于點![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() 在直線
在直線![]() 上,∴
上,∴![]() ,
,
∴![]() ,則
,則![]() .
.
(2)當![]() 時,
時,![]() 為
為![]() ,此時
,此時![]() ,
,
∴![]() 的軌跡為以
的軌跡為以![]() 、
、![]() 為焦點的橢圓,其中
為焦點的橢圓,其中![]() ,
,![]() ,
,![]() ,
,
∴橢圓![]() 的方程為
的方程為![]() .
.
∵![]() 為右頂點,∴
為右頂點,∴![]() 為
為![]() ,設
,設![]() ,
,![]() ,
,
![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
即![]() ,①
,①
∵![]() ,
,![]() 在直線
在直線![]() 上,
上,
∴①式變?yōu)?/span>![]() ,②
,②
聯立直線方程與橢圓方程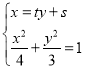 ,
,
得![]() ,
,
∴![]() ,
,![]() ,
,
代入②式得![]() ,∴
,∴![]() 或
或![]() ,
,
當![]() 時,
時,![]() 、
、![]() 或
或![]() 、
、![]() 重合,
重合,
與![]() 、
、![]() 為非零向量矛盾,舍去.
為非零向量矛盾,舍去.
∴![]() ,直線
,直線![]() 為
為![]() ,過定點
,過定點![]() ,
,
此時![]()
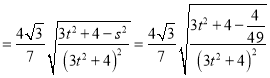
令![]() ,則
,則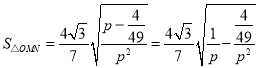 ,
,
∵![]() ,∴
,∴![]() ,
,
即![]() 時,
時,![]() 有最大值,最大值為
有最大值,最大值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】 (2017·黃岡質檢)如圖,在棱長均為2的正四棱錐P-ABCD中,點E為PC的中點,則下列命題正確的是( )

A.BE∥平面PAD,且BE到平面PAD的距離為![]()
B.BE∥平面PAD,且BE到平面PAD的距離為![]()
C.BE與平面PAD不平行,且BE與平面PAD所成的角大于30°
D.BE與平面PAD不平行,且BE與平面PAD所成的角小于30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在學校組織的英語單詞背誦比賽中,5位評委對甲、乙兩名同學的評分如莖葉圖所示(分數為整數,且滿分100分),若甲同學所得評分的中位數為87,乙同學所得評分的唯一眾數為86,則甲同學所得評分的平均數不小于乙同學所得評分的平均數的概率為______.
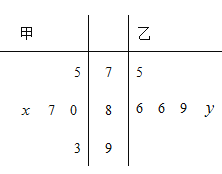
查看答案和解析>>
科目:高中數學 來源: 題型:
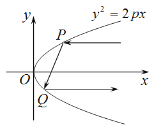
【題目】拋物線有如下光學性質:由其焦點射出的光線經拋物線反射后,沿平行于拋物線對稱軸的方向射出.現有拋物線![]() ,如圖一平行于
,如圖一平行于![]() 軸的光線射向拋物線,經兩次反射后沿平行
軸的光線射向拋物線,經兩次反射后沿平行![]() 軸方向射出,若兩平行光線間的最小距離為4,則該拋物線的方程為__________.
軸方向射出,若兩平行光線間的最小距離為4,則該拋物線的方程為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型工廠有![]() 臺大型機器,在
臺大型機器,在![]() 個月中,
個月中,![]() 臺機器至多出現
臺機器至多出現![]() 次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需
次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需![]() 名工人進行維修.每臺機器出現故障的概率為
名工人進行維修.每臺機器出現故障的概率為![]() .已知
.已知![]() 名工人每月只有維修
名工人每月只有維修![]() 臺機器的能力,每臺機器不出現故障或出現故障時有工人維修,就能使該廠獲得
臺機器的能力,每臺機器不出現故障或出現故障時有工人維修,就能使該廠獲得![]() 萬元的利潤,否則將虧損
萬元的利潤,否則將虧損![]() 萬元.該工廠每月需支付給每名維修工人
萬元.該工廠每月需支付給每名維修工人![]() 萬元的工資.
萬元的工資.
(1)若每臺機器在當月不出現故障或出現故障時有工人進行維修,則稱工廠能正常運行.若該廠只有![]() 名維修工人,求工廠每月能正常運行的概率;
名維修工人,求工廠每月能正常運行的概率;
(2)已知該廠現有![]() 名維修工人.
名維修工人.
(ⅰ)記該廠每月獲利為![]() 萬元,求
萬元,求![]() 的分布列與數學期望;
的分布列與數學期望;
(ⅱ)以工廠每月獲利的數學期望為決策依據,試問該廠是否應再招聘![]() 名維修工人?
名維修工人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列有關命題的說法錯誤的是( )
A.若“p∨q”為假命題,則p,q均為假命題
B.“x=1”是“x≥1”的充分不必要條件
C.“sinx=![]() ”的必要不充分條件是“x=
”的必要不充分條件是“x=![]() ”
”
D.若命題p:x0∈R,x02≥0,則命題¬p:x∈R,x2<0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的個數是( )
①一組數據的標準差越大,則說明這組數據越集中;
②曲線![]() 與曲線
與曲線![]() 的焦距相等;
的焦距相等;
③在頻率分布直方圖中,估計的中位數左邊和右邊的直方圖的面積相等;
④已知橢圓![]() ,過點
,過點![]() 作直線,當直線斜率為
作直線,當直線斜率為![]() 時,M剛好是直線被橢圓截得的弦AB的中點.
時,M剛好是直線被橢圓截得的弦AB的中點.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=a![]() +bx-a-ab(a≠0),當
+bx-a-ab(a≠0),當![]() 時,f(x)>0;當
時,f(x)>0;當![]() 時,f(x)<0.
時,f(x)<0.
(1)求f(x)在![]() 內的值域;
內的值域;
(2)若方程![]() 在
在![]() 有兩個不等實根,求c的取值范圍.
有兩個不等實根,求c的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com