
【題目】已知C是以AB為直徑的圓周上一點,![]() 平面
平面![]() .
.
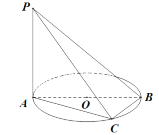
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若異面直線PB與AC所成的為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)由線面垂直的性質定理可知![]() .再由
.再由![]() 以及線面垂直的判斷定理,可知
以及線面垂直的判斷定理,可知![]() 平面
平面![]() ,即可證明.
,即可證明.
(2)解法1,建立空間直角坐標系,令![]() ,確定點坐標,令
,確定點坐標,令![]()
![]() ,由題意可知
,由題意可知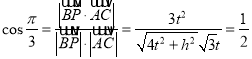 ,即
,即![]() ,再求平面
,再求平面![]() 的法向量為
的法向量為![]() 與平面
與平面![]() 的法向量為
的法向量為![]() ,求解
,求解![]() 即可.解法2:過
即可.解法2:過![]() 作
作![]() 的平行線
的平行線![]() 交圓于
交圓于![]() ,連接
,連接![]() ,
,![]() ,所以直線
,所以直線![]() 與
與![]() 所成的角,即為
所成的角,即為![]() 與
與![]() 所成的角,
所成的角,![]() ,再過
,再過![]() 作
作![]() 交
交![]() 于
于![]() ,過
,過![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,由三垂線定理知
,由三垂線定理知![]() ,所以
,所以![]() 即為二面角
即為二面角![]() 的平面角,求解邊長即可.
的平面角,求解邊長即可.
(1)證明:因為![]() 為圓的直徑,所以
為圓的直徑,所以![]() ,
,
又![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() 平面
平面![]() ;
;
(2)解法1:建系如圖所示
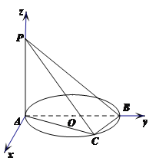
令![]() ,而
,而![]() ,則
,則![]() ,
,![]() .
.
則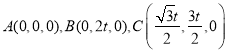 ,令
,令![]()
![]()
所以![]() ,
,![]() .
.
因為異面直線![]() 與
與![]() 所成的角為
所成的角為![]()
故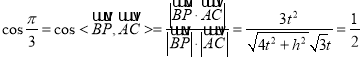 ,解得
,解得![]() .
.
令平面![]() 的一個法向量為
的一個法向量為![]()
而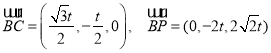
由![]()
![]() ,
,![]() ,所以
,所以![]()
由![]() ,
,![]() ,所以
,所以![]() ,即
,即![]()
而平面![]() 的一個法向量為
的一個法向量為![]()
所以 .
.
所以二面角![]() 的余弦值為
的余弦值為![]()
解法2:過![]() 作
作![]() 的平行線
的平行線![]() 交圓于
交圓于![]() ,連接
,連接![]() ,
,![]()
所以直線![]() 與
與![]() 所成的角,即為
所成的角,即為![]() 與
與![]() 所成的角.
所成的角.
因為![]() 為圓的直徑,所以
為圓的直徑,所以![]()
又![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]()
而![]() 平面
平面![]() ,所以
,所以![]() ,則
,則![]() .
.
令![]() ,且
,且![]() 所以
所以![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
過![]() 作
作![]() 交
交![]() 于
于![]() ,過
,過![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,由三垂線定理知
,由三垂線定理知![]() .
.
所以![]() 即為二面角
即為二面角![]() 的平面角.
的平面角.
![]() ,
,![]()
![]() 即
即 ![]() .
.
即為二面角![]() 的余弦值為
的余弦值為![]() .
.


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:
【題目】狄利克雷函數是高等數學中的一個典型函數,若![]() ,則稱
,則稱![]() 為狄利克雷函數.對于狄利克雷函數
為狄利克雷函數.對于狄利克雷函數![]() ,給出下面4個命題:①對任意
,給出下面4個命題:①對任意![]() ,都有
,都有![]() ;②對任意
;②對任意![]() ,都有
,都有![]() ;③對任意
;③對任意![]() ,都有
,都有![]() ,
, ![]() ;④對任意
;④對任意![]() ,都有
,都有![]() .其中所有真命題的序號是( )
.其中所有真命題的序號是( )
A. ①④ B. ②③ C. ①②③ D. ①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學著作《算法統宗》中記載了這樣的一個問題:“三百七十八里關,初行健步不為難,次日腳痛減一半,六朝才得到其關,要見次日行里數,請公仔細算相還”,其大意為:有一個人走了378里路,第一天健步行走,從第二天起其因腳痛每天走的路程為前一天的一半,走了6天后到達了目的地,問此人第三天走的路程里數為( )
A.192B.48C.24D.88
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的坐標為
的坐標為![]() ,若點
,若點![]() 是曲線
是曲線![]() 截直線
截直線![]() 所得線段的中點,求
所得線段的中點,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個不透明的盒子中關有蝴蝶、蜜蜂和蜻蜓三種昆蟲共11只,現在盒子上開一小孔,每次只能飛出1只昆蟲(假設任意1只昆蟲等可能地飛出).若有2只昆蟲先后任意飛出(不考慮順序),則飛出的是蝴蝶或蜻蜓的概率是![]() .
.
(1)求盒子中蜜蜂有幾只;
(2)若從盒子中先后任意飛出3只昆蟲(不考慮順序),記飛出蜜蜂的只數為X,求隨機變量X的分布列與數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+1,g(x)=4x+1,的定義域都是集合A,函數f(x)和g(x)的值域分別為S和T,
(1)若A=[1,2],求S∩T
(2)若A=[0,m]且S=T,求實數m的值
(3)若對于集合A的任意一個數x的值都有f(x)=g(x),求集合A.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】工人在安裝一個正六邊形零件時,需要固定如圖所示的六個位置的螺絲,第一階段,首先隨意擰一個螺絲,接著擰它對角線上(距離它最遠的,下同)螺絲,再隨意擰第三個螺絲,第四個也擰它對角線上螺絲,第五個和第六個以此類推,但每個螺絲都不要擰死;第二階段,將每個螺絲擰死,但不能連續擰相鄰的2個螺絲.則不同的固定方式有________.
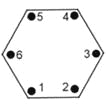
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com