
【題目】如圖,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,以橢圓
,以橢圓![]() 的左頂點
的左頂點![]() 為圓心作圓
為圓心作圓![]() :
:![]() ,設圓
,設圓![]() 與橢圓
與橢圓![]() 交于點
交于點![]() 與點
與點![]() .
.
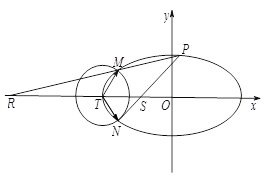
(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 的最小值,并求此時圓
的最小值,并求此時圓![]() 的方程;
的方程;
(3)設點![]() 是橢圓
是橢圓![]() 上異于
上異于![]() ,
,![]() 的任意一點,且直線
的任意一點,且直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,
,![]() 為坐標原點,
為坐標原點,
求證:![]() 為定值.
為定值.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,證明見解析.
,證明見解析.
【解析】
試題(1)先通過離心率求出![]() ,再通過
,再通過![]() ,然后寫出橢圓方程;(2)先設出
,然后寫出橢圓方程;(2)先設出![]() 點的坐標,由于點
點的坐標,由于點![]() 在橢圓
在橢圓![]() 上,所以
上,所以![]() ,找到
,找到![]() 向量坐標,根據點乘列出表達式,配方法找到表達式的最小值,得到
向量坐標,根據點乘列出表達式,配方法找到表達式的最小值,得到![]() 點坐標,點
點坐標,點![]() 在圓上,代入得到圓的半徑,就可以得到圓的方程;(3)設出點
在圓上,代入得到圓的半徑,就可以得到圓的方程;(3)設出點![]() 的坐標,列出直線
的坐標,列出直線![]() 的方程,因為直線與
的方程,因為直線與![]() 軸有交點,所以令
軸有交點,所以令![]() ,得到
,得到![]() ,所以
,所以![]() ,又因為點
,又因為點![]() 在橢圓上,得到方程,代入
在橢圓上,得到方程,代入![]() 中,得到
中,得到![]() ,所以
,所以![]() .
.
試題解析:(1)依題意,得![]() ,
,![]() ,∴
,∴![]() ;
;
故橢圓![]() 的方程為
的方程為![]() . 3分
. 3分
(2)方法一:點![]() 與點
與點![]() 關于
關于![]() 軸對稱,設
軸對稱,設![]() ,
,![]() , 不妨設
, 不妨設![]() .
.
由于點![]() 在橢圓
在橢圓![]() 上,所以
上,所以![]() . (*) 4分
. (*) 4分
由已知![]() ,則
,則![]() ,
,![]() ,
,
所以![]()
![]()
![]() . 6分
. 6分
由于![]() ,故當
,故當![]() 時,
時,![]() 取得最小值為
取得最小值為![]() .
.
由(*)式,![]() ,故
,故![]() ,又點
,又點![]() 在圓
在圓![]() 上,代入圓的方程得到
上,代入圓的方程得到![]() .
.
故圓![]() 的方程為:
的方程為:![]() . 8分
. 8分
方法二:點![]() 與點
與點![]() 關于
關于![]() 軸對稱,故設
軸對稱,故設![]() ,
,
不妨設![]() ,由已知
,由已知![]() ,則
,則
![]()
![]()
![]() . 6分
. 6分
故當![]() 時,
時,![]() 取得最小值為
取得最小值為![]() ,此時
,此時![]() ,
,
又點![]() 在圓
在圓![]() 上,代入圓的方程得到
上,代入圓的方程得到![]() .
.
故圓![]() 的方程為:
的方程為:![]() . 8分
. 8分
(3) 方法一:設![]() ,則直線
,則直線![]() 的方程為:
的方程為:![]() ,
,
令![]() ,得
,得![]() , 同理:
, 同理:![]() , 10分
, 10分
故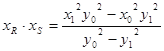 (**) 11分
(**) 11分
又點![]() 與點
與點![]() 在橢圓上,故
在橢圓上,故![]() ,
,![]() , 12分
, 12分
代入(**)式,得: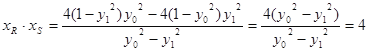 .
.
所以![]() 為定值. 14分
為定值. 14分
方法二:設![]() ,不妨設
,不妨設![]() ,
,![]() ,
,
其中![]() .則直線
.則直線![]() 的方程為:
的方程為:![]() ,
,
令![]() ,得
,得![]() ,
,
同理:![]() , 12分
, 12分
故![]() .
.
所以![]() 為定值. 14分
為定值. 14分


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知奇函數f(x)![]() ,函數g(θ)=cos2θ+2sinθ
,函數g(θ)=cos2θ+2sinθ![]() ,θ∈[m,
,θ∈[m,![]() ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判斷函數f(x)在[0,1]上的單調性,并證明;
(3)當x∈[0,1]時,函數g(θ)的最小值恰為f(x)的最大值,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】階梯水價的原則是“保基本、建機制、促節約”,其中“保基本”是指保證至少80%的居民用戶用水價格不變.為響應國家政策,制訂合理的階梯用水價格,某城市采用簡單隨機抽樣的方法分別從郊區和城區抽取5戶和20戶居民的年人均用水量進行調研,得到數據如下(單位:噸).
郊區:19 25 28 32 34
城區:18 19 21 22 22 23 23 23 24 25 26 27 28 28 28 29 29 31 35 42
(1)在郊區的這5戶居民中隨機抽取2戶,求其年人均用水量都不超過30噸的概率;
(2)設該城市郊區和城區的居民戶數比為1:5,現將年人均用水量不超過30噸的用戶定義為第一階梯用戶,并保證這一階梯的居民用戶用水價格保持不變,試根據樣本總體的思想,分析此方案是否符合國家“保基本”政策.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】調查某校高三年級男生的身高,隨機抽取40名高三男生,實測身高數據(單位:cm)如下:
171 | 163 | 163 | 166 | 166 | 168 | 168 | 160 | 168 | 165 |
171 | 169 | 167 | 169 | 151 | 168 | 170 | 168 | 160 | 174 |
165 | 168 | 174 | 159 | 167 | 156 | 157 | 164 | 169 | 180 |
176 | 157 | 162 | 161 | 158 | 164 | 163 | 163 | 167 | 161 |
(1)作出頻率分布表;
(2)畫出頻率分布直方圖.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出如圖所示的三幅統計圖及四個命題:
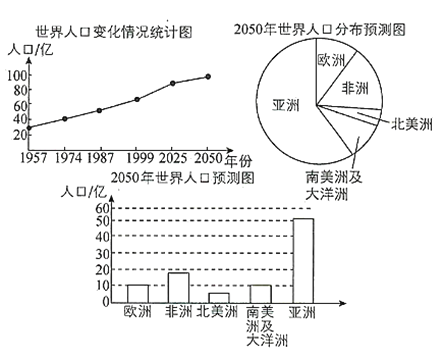
①從折線圖能看出世界人口的變化情況;
②2050年非洲人口將達到大約15億;
③2050年亞洲人口比其他各洲人口的總和還要多;
④從1957年到2050年各洲中北美洲人口增長速度最慢.
其中命題正確的有( )
A.①②B.①③C.①④D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】12個朋友每周聚餐一次,每周他們分成三組,每組4人,不同組坐不同的桌子.若要求這些朋友中任意兩個人至少有一次同坐一張桌子,則至少需要周____周.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是自然數1,2,…,
是自然數1,2,…,![]() 的一個排列,且滿足:對任意
的一個排列,且滿足:對任意![]() ,均有
,均有![]() .
.
(1)若記![]() 為數
為數![]() 在排列中所處位置的序號(如排列
在排列中所處位置的序號(如排列![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ).求證:對每一個滿足題意的排列
).求證:對每一個滿足題意的排列![]() ,均有
,均有![]() 成立.
成立.
(2)試求滿足題意的排列的個數![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 定義域為
定義域為![]() ,部分對應值如表,
,部分對應值如表,![]() 的導函數
的導函數![]() 的圖象如圖所示. 下列關于函數
的圖象如圖所示. 下列關于函數![]() 的結論正確的有( )
的結論正確的有( )
|
|
|
|
|
|
|
|
|
|
|
|

A.函數![]() 的極大值點有
的極大值點有![]() 個
個
B.函數在![]() 上
上![]() 是減函數
是減函數
C.若![]() 時,
時,![]() 的最大值是
的最大值是![]() ,則
,則![]() 的最大值為4
的最大值為4
D.當![]() 時,函數
時,函數![]() 有
有![]() 個零點
個零點
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com