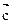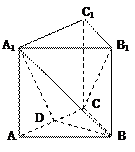已知點

在同一個球面上,

平面

,

,若

,


,

,則

兩點間的球面距離是
.

因為

,所以
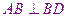
,所以
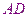
為球的直徑,其中點為球心,連接
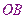
和
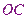
,則
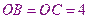
,
在
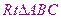
中,因為
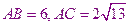
,所以
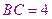
,
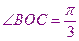
,故則
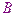
、
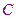
兩點間的球面距離是

.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
α、β是兩個不同的平面,m,n是平面α及β之外的兩條不同直線,給出四個論斷:①m⊥n,②α⊥β,③n⊥β,④m⊥α.以其中三個論斷作為條件,余下的一個論斷作為結論,寫出你認為正確的一個命題,并證明它.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,斜三棱柱
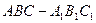
的所有棱長均為
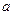
,側面
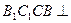
底面
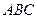
,且
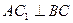
.
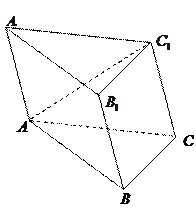
(1)求異面直線
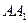
與
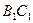
間的距離;
(2)求側面
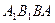
與底面
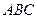
所成二面角的度數(shù).
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
過正方體外接球球心的截面截正方體所得圖形可能為 (填序號)①三角形 ②正方形 ③梯形 ④五邊形 ⑤六邊形
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在四棱錐
P-
ABCD中,∠
ABC=∠
ACD=90°,∠
BAC=∠
CAD=60°,
PA⊥平面
ABCD,
E為
PD的中點,
PA=2
AB=2.(Ⅰ)求四棱錐
P-
ABCD的體積
V;

(Ⅱ)若
F為
PC的中點,求證
PC⊥平面
AEF;
(Ⅲ)求證
CE∥平面
PAB.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
命題①空間直線a,b,c,若a∥b,b∥c則a∥c
②非零向量
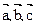
,若
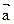
∥
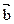
,
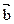
∥
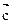
則
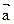
∥
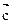
③平面α、β、γ若α⊥β,β⊥γ,則α∥γ
④空間直線a、b、c若有a⊥b,b⊥c,則a∥c
⑤直線a、b與平面β,若a⊥β,c⊥β,則a∥c
其中所有真命題的序號是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知正四棱柱

,點
P是棱
DD1的中點,

,
AB=1,若點
Q在側面

(包括其邊界)上運動,且總保持

,則動點
Q的軌跡是 ( )

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題12分)
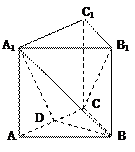
如圖,正三棱柱ABC-A
1B
1C
1的底面邊長是2, 側棱長是, D為AC的中點.
(1)求證: B
1C∥平面A
1BD
(2)求二面角A
1-BD-A的大小.
(3)求直線AB
1與平面A
1BD所成角的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知四棱錐的側棱都相等,那么四棱錐的底面( )
| A.存在外接圓 | B.存在內切圓 | C.為正方形 | D.為矩形 |
查看答案和解析>>

 在同一個球面上,
在同一個球面上,  平面
平面 ,
, ,若
,若 ,
,
 ,
, ,則
,則 兩點間的球面距離是 .
兩點間的球面距離是 .

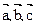 ,若
,若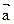 ∥
∥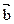 ,
,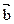 ∥
∥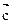 則
則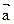 ∥
∥