Question

【題目】已知函數.

（Ⅰ）若是函數是極值點，1是函數零點，求實數，的值和函數的單調區間；

（Ⅱ） 若對任意，都存在（為自然對數的底數），使得成立，求實數的取值范圍.

Answer 1

【答案】（1）見解析（2）見解析

【解析】 試題分析: （1）對求導, ,利用已知條件x=2是函數極值點,1是函數零點,可得a,b的值,進而得到的單調區間; （2）構造函數,由b的范圍及其范圍內的任意性將問題轉化為存在,使得,對求導并構造函數,利用分類討論的方法研究兩種情況下的函數正負,最終證明當a>1時,對任意,都存在,使得成立.

試題解析:解：（Ⅰ）.

∵是函數的極值點，∴.

又∵1是函數的零點，∴.

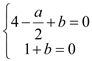聯立，解得：，∴，

，.

∵在，，∴在（0,2）上單調遞減；又在，，

∴在上單調遞增.

（Ⅱ）令，，則為關于的一次函數且為增函數，

∴要使成立，只需在有解.

令：，只需存在，使得.

由于，，

令：，∴，

∴在遞增，∴.

（ⅰ）當時，，即，

∴在是單調遞增，∴，不合題意.

（ⅱ）當時，，

若，則上單調遞減，

∴存在，使得，符合題意.

若，則，即，

∴存在使得.

∴在上成立，∴在上單調遞減，

∴存在使得成立.

綜上所述：當時，對任意，都存在使得.