
【題目】如圖,三棱錐P﹣ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一點(diǎn),且CD⊥平面PAB.
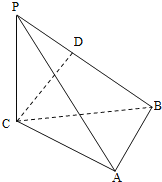
(1)求證:AB⊥平面PCB;
(2)求二面角C﹣PA﹣B的大小的余弦值.
【答案】(1)詳見(jiàn)解析;(2)![]() .
.
【解析】
( 1)由題設(shè)條件,易證得PC⊥AB,CD⊥AB,故可由線面垂直的判定定理證得AB⊥平面PCB;(2)由圖形知,取AP的中點(diǎn)O,連接CO、DO,可證得∠COD為二面角C﹣PA﹣B的平面角,在△CDO中求∠COD即可.
(1)證明:∵PC⊥平面ABC,AB平面ABC,
∴PC⊥AB.
∵CD⊥平面PAB,AB平面PAB,
∴CD⊥AB.又PC∩CD=C,∴AB⊥平面PCB.
(2)取AP的中點(diǎn)O,連接CO、DO.
∵PC=AC=2,∴CO⊥PA,CO![]() ,
,
∵CD⊥平面PAB,由三垂線定理的逆定理,得DO⊥PA.
∴∠COD為二面角C﹣PA﹣B的平面角.
由(1)AB⊥平面PCB,∴AB⊥BC,
又∵AB=BC,AC=2,求得BC![]()
PB![]() ,CD
,CD![]()
∴![]()
cos∠COD![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司為確定下一年度投入某種產(chǎn)品的宣傳費(fèi),需了解年宣傳費(fèi)對(duì)年銷(xiāo)售量(單位:t)的影響.該公司對(duì)近5年的年宣傳費(fèi)和年銷(xiāo)售量數(shù)據(jù)進(jìn)行了研究,發(fā)現(xiàn)年宣傳費(fèi)x(萬(wàn)元)和年銷(xiāo)售量y(單位:t)具有線性相關(guān)關(guān)系,并對(duì)數(shù)據(jù)作了初步處理,得到下面的一些統(tǒng)計(jì)量的值.

(1)根據(jù)表中數(shù)據(jù)建立年銷(xiāo)售量y關(guān)于年宣傳費(fèi)x的回歸方程;
(2)已知這種產(chǎn)品的年利潤(rùn)z與x,y的關(guān)系為![]() ,根據(jù)(1)中的結(jié)果回答下列問(wèn)題:
,根據(jù)(1)中的結(jié)果回答下列問(wèn)題:
①當(dāng)年宣傳費(fèi)為10萬(wàn)元時(shí),年銷(xiāo)售量及年利潤(rùn)的預(yù)報(bào)值是多少?
②估算該公司應(yīng)該投入多少宣傳費(fèi),才能使得年利潤(rùn)與年宣傳費(fèi)的比值最大.
附:回歸方程![]() 中的斜率和截距的最小二乘估計(jì)公式分別為
中的斜率和截距的最小二乘估計(jì)公式分別為

參考數(shù)據(jù):![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,等腰![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的四等分點(diǎn),且
的四等分點(diǎn),且![]() .現(xiàn)沿
.現(xiàn)沿![]() ,
,![]() ,
,![]() 折疊成圖2所示的幾何體,使
折疊成圖2所示的幾何體,使![]() .
.
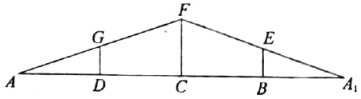
(圖1)
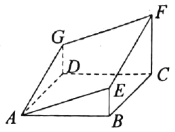
(圖2)
(1)證明:![]() 平面
平面![]() ;
;
(2)求幾何體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在極坐標(biāo)系中,已知曲線![]() 的方程為
的方程為![]() ,曲線
,曲線![]() 的方程為
的方程為![]() .以極點(diǎn)
.以極點(diǎn)![]() 為原點(diǎn),極軸為
為原點(diǎn),極軸為![]() 軸正半軸建立直角坐標(biāo)系
軸正半軸建立直角坐標(biāo)系![]() .
.
(1)求曲線![]() ,
,![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若曲線![]() 與
與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() ,與曲線
,與曲線![]() 相交于
相交于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某城市為了解游客人數(shù)的變化規(guī)律,提高旅游服務(wù)質(zhì)量,收集并整理了2017年1月至2019年12月期間月接待游客量(單位:萬(wàn)人)的數(shù)據(jù),繪制了下面的折線圖.根據(jù)該折線圖,下列結(jié)論錯(cuò)誤的是( )

A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位數(shù)為30萬(wàn)人
D.各年1月至6月的月接待游客量相對(duì)于7月至12月,波動(dòng)性更小,變化比較平穩(wěn)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在底面為正方形的四棱錐![]() 中,
中,![]() 平面
平面![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別在棱
分別在棱![]() ,
,![]() 上,且滿足
上,且滿足![]() ,
,![]() .
.
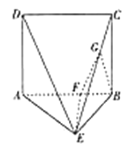
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)![]() 、
、![]() 為雙曲線
為雙曲線![]()
![]() 的左、右焦點(diǎn),過(guò)
的左、右焦點(diǎn),過(guò)![]() 作垂直于
作垂直于![]() 軸的直線,在
軸的直線,在![]() 軸上方交雙曲線
軸上方交雙曲線![]() 于點(diǎn)
于點(diǎn)![]() ,且
,且![]() ,圓
,圓![]() 的方程是
的方程是![]() .
.
(1)求雙曲線![]() 的方程;
的方程;
(2)過(guò)雙曲線![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() 作該雙曲線兩條漸近線的垂線,垂足分別為
作該雙曲線兩條漸近線的垂線,垂足分別為![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)過(guò)圓![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() 作圓
作圓![]() 的切線
的切線![]() 交雙曲線
交雙曲線![]() 于
于![]() 、
、![]() 兩點(diǎn),
兩點(diǎn),![]() 中點(diǎn)為
中點(diǎn)為![]() ,求證:
,求證:![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 有兩個(gè)零點(diǎn)
有兩個(gè)零點(diǎn)![]() ,有一個(gè)極值點(diǎn)
,有一個(gè)極值點(diǎn)![]() .
.
(1)求實(shí)數(shù)a的取值范圍;
(2)求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)年利率為![]() 的連續(xù)復(fù)利,要在
的連續(xù)復(fù)利,要在![]() 年后達(dá)到本利和
年后達(dá)到本利和![]() ,則現(xiàn)在投資值為
,則現(xiàn)在投資值為![]() ,
,![]() 是自然對(duì)數(shù)的底數(shù).如果項(xiàng)目
是自然對(duì)數(shù)的底數(shù).如果項(xiàng)目![]() 的投資年利率為
的投資年利率為![]() 的連續(xù)復(fù)利.
的連續(xù)復(fù)利.
(1)現(xiàn)在投資5萬(wàn)元,寫(xiě)出滿![]() 年的本利和,并求滿10年的本利和;(精確到0.1萬(wàn)元)
年的本利和,并求滿10年的本利和;(精確到0.1萬(wàn)元)
(2)一個(gè)家庭為剛出生的孩子設(shè)立創(chuàng)業(yè)基金,若每年初一次性給項(xiàng)目![]() 投資2萬(wàn)元,那么,至少滿多少年基金共有本利和超過(guò)一百萬(wàn)元?(精確到1年)
投資2萬(wàn)元,那么,至少滿多少年基金共有本利和超過(guò)一百萬(wàn)元?(精確到1年)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com