
【題目】已知AB是圓O的直徑,C,D是圓上不同兩點,且CD∩AB=H,AC=AD,PA⊥圓O所在平面.
(Ⅰ)求證:PB⊥CD;
(Ⅱ)若PB=![]() ,∠PBA=
,∠PBA=![]() ,∠CAD=
,∠CAD=![]() ,求H到平面PBD的距離.
,求H到平面PBD的距離.
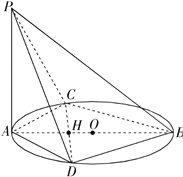
【答案】(Ⅰ)證明見解析;(Ⅱ) ![]() .
.
【解析】試題分析:(Ⅰ)由AB是圓O的直徑知∠ACB=∠ADB=90°,從而證明PB⊥CD.(Ⅱ)過點P作PB的垂線,過點H作PB的垂線,分別交PB于點E,F;求出H到平面PBD的距離.
試題解析:
(Ⅰ)證明:∵AB是圓O的直徑,
∴∠ACB=∠ADB=![]() ,
,
∵AC=AD,∴Rt△ACB≌Rt△ADB,∴AB⊥CD,
又∵PA⊥圓O所在平面,CD在圓O所在平面內,
∴PA⊥CD,
∵PA∩AB=A,∴CD⊥平面PAB,∴PB⊥CD.
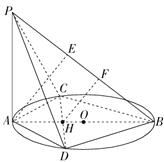
(Ⅱ)解:過點A作PB的垂線,過點H作PB的垂線,分別交PB于E,F,
∵Rt△PAB中,∠PBA=![]() ,PB=2
,PB=2![]() ,
,
∴PA=AB=2,∴AE=ABsin![]() =2·
=2·![]() =
=![]() ,
,
又∵∠CAB=∠DAB=![]() ,∴AC=1,AD=1
,∴AC=1,AD=1
∵CH⊥AH,∴AH=![]() ,
,
∴BH=![]() ,HD=
,HD=![]() ,BD=
,BD=![]() ,PD=
,PD=![]()
∴VH-PBD=VP-HDB=![]() ×
×![]() ×
×![]() ×
×![]() ×2=
×2=![]()
S△PBD=![]() ×
×![]() ×
×![]() =
=![]() ,
,
∴H到平面PBD的距離為![]() =
=![]() .
.


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案科目:高中數學 來源: 題型:
【題目】某公司研制出了一種新產品,試制了一批樣品分別在國內和國外上市銷售,并且價格根據銷售情況不斷進行調整,結果40天內全部銷完.公司對銷售及銷售利潤進行了調研,結果如圖所示,其中圖①(一條折線)、圖②(一條拋物線段)分別是國外和國內市場的日銷售量與上市時間的關系,圖③是每件樣品的銷售利潤與上市時間的關系.

(1)分別寫出國外市場的日銷售量f(t)與上市時間t的關系及國內市場的日銷售量g(t)與上市時間t的關系;
(2)國外和國內的日銷售利潤之和有沒有可能恰好等于6 300萬元?若有,請說明是上市后的第幾天;若沒有,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|ax-2|.
(1)當a=2時,解不等式f(x)>x+1;
(2)若關于x的不等式f(x)+f(-x)< ![]() 有實數解,求m的取值范圍.
有實數解,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某運輸公司接受了向一地區每天至少運送180 t物資的任務,該公司有8輛載重為6 t的A型卡車和4輛載重為10 t的B型卡車,有10名駕駛員,每輛卡車每天往返的次數為A型卡車4次,B型卡車3次,每輛卡車每天往返的費用為A型卡車320元,B型卡車504元,則公司如何調配車輛,才能使公司所花的費用最低,最低費用為________元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)及其導數f′(x),若存在x0,使得f(x0)=f′(x0),則稱x0是f(x)的一個“巧值點”,則下列函數中有“巧值點”的是________.
①f(x)=x2;②f(x)=e-x;③f(x)=lnx;④f(x)=tanx;⑤![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2016·山東)設f(x)=xlnx-ax2+(2a-1)x,a∈R.
(1)令g(x)=f′(x),求g(x)的單調區間;
(2)已知f(x)在x=1處取得極大值,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·洛陽市統考)已知數列{an}的前n項和為Sn,an≠0,a1=1,且2anan+1=4Sn-3(n∈N*).
(1)求a2的值并證明:an+2-an=2;
(2)求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C的參數方程為![]() (α為參數),直線l的參數方程為
(α為參數),直線l的參數方程為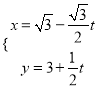 (t為參數),在以坐標原點O為極點,x軸正半軸為極軸的極坐標系中,過極點O的射線與曲線C相交于不同于極點的點A,且點A的極坐標為(2
(t為參數),在以坐標原點O為極點,x軸正半軸為極軸的極坐標系中,過極點O的射線與曲線C相交于不同于極點的點A,且點A的極坐標為(2![]() ,θ),其中θ∈
,θ),其中θ∈![]() .
.
(1)求θ的值;
(2)若射線OA與直線l相交于點B,求|AB|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com