
【題目】已知A、B、C三個箱子中各裝有2個完全相同的球,每個箱子里的球,有一個球標著號碼1,另一個球標著號碼2.現從A、B、C三個箱子中各摸出1個球.
(Ⅰ)若用數組![]() 中的
中的![]() 分別表示從A、B、C三個箱子中摸出的球的號碼,請寫出數組
分別表示從A、B、C三個箱子中摸出的球的號碼,請寫出數組![]() 的所有情形,并回答一共有多少種;
的所有情形,并回答一共有多少種;
(Ⅱ)如果請您猜測摸出的這三個球的號碼之和,猜中有獎.那么猜什么數獲獎的可能性最大?請說明理由.
【答案】(1)(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2),共8種
(2)猜4或5獲獎的可能性最大
【解析】
第一問中,先分析所有的情況為共有8種,
第二問,由于事件![]() 包含1個基本事件,事件
包含1個基本事件,事件![]() 包含3個基本事件,事件
包含3個基本事件,事件![]() 包含3個基本事件,事件
包含3個基本事件,事件![]() 包含1個基本事件,然后利用古典概型的概率計算公式得到,比較大小即可.
包含1個基本事件,然后利用古典概型的概率計算公式得到,比較大小即可.
解:(Ⅰ)數組![]() 的所有情形為:(1,1,1),(1,1,2),(1,2,1),
的所有情形為:(1,1,1),(1,1,2),(1,2,1),
(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2),共8種.
答:一共有8種. ………………………5分
注:列出5、6、7種情形,得2分;列出所有情形,得4分;寫出所有情形共8種,得1分.
(Ⅱ)記“所摸出的三個球號碼之和為![]() ”為事件
”為事件![]() (
(![]() =3,4,5,6), ………6分
=3,4,5,6), ………6分
易知,事件![]() 包含1個基本事件,事件
包含1個基本事件,事件![]() 包含3個基本事件,事件
包含3個基本事件,事件![]() 包含3個基本事件,事件
包含3個基本事件,事件![]() 包含1個基本事件,所以,
包含1個基本事件,所以,
![]() ,
,![]() ,
,![]() ,
,![]() . ……………………10分
. ……………………10分
故所摸出的兩球號碼之和為4、為5的概率相等且最大.
答:猜4或5獲獎的可能性最大. ……………………12分


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:高中數學 來源: 題型:
【題目】下列命題中正確的是( )
A.若p∨q為真命題,則p∧q為真命題
B.“x=5”是“x2-4x-5=0”的充分不必要條件
C.命題“若x<-1,則x2-2x-3>0”的否定為:“若x≥-1,則x2-2x-3≤0”
D.已知命題p:x∈R,x2+x-1<0,則![]() p:x∈R,x2+x-1≥0
p:x∈R,x2+x-1≥0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(題文)
等邊△ABC的邊長為3,點D,E分別為AB,AC上的點,且滿足![]() (如圖①),將△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,連接A1B,A1C(如圖②).
(如圖①),將△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,連接A1B,A1C(如圖②).
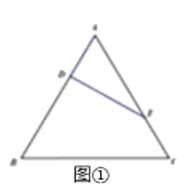
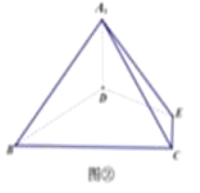
(1)求證:A1D⊥平面BCED;
(2)在線段BC上是否存在點P(不包括端點),使直線PA1與平面A1BD所成的角為60°?若存在,求出A1P的長,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() 為直線
為直線![]() 的傾斜角),以坐標原點
的傾斜角),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的直角坐標方程,并求
的直角坐標方程,并求![]() 時直線
時直線![]() 的普通方程;
的普通方程;
(2)直線![]() 和曲線
和曲線![]() 交于兩點
交于兩點![]() ,點
,點![]() 的直角坐標為
的直角坐標為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求函數
,求函數![]() 在
在![]() 的單調區間;
的單調區間;
(Ⅱ)方程![]() 有3個不同的實根,求實數
有3個不同的實根,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)當![]() 時,若對于任意的
時,若對于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求滿足條件的正整數
,求滿足條件的正整數![]() 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,已知橢圓的長軸為
的左、右焦點,已知橢圓的長軸為![]() 是橢圓
是橢圓![]() 上一動點,
上一動點,![]() 的最大值為
的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,
兩點,![]() 為橢圓
為橢圓![]() 上一點,
上一點,![]() 為坐標原點,且滿足
為坐標原點,且滿足![]() ,其中
,其中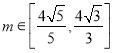 ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xex,g(x)=a(lnx+x).
(1)當a=e時,求證:f(x)≥g(x)恒成立;
(2)當a>0時,求證:f(x)≤g(x)+1恒有解.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:x∈[1,2],log2(x+2)<2m;命題q:關于x的方程x2﹣x+m2=0有兩個不同的實數根.
(1)若(¬p)∧q為真命題,求實數m的取值范圍;
(2)若p∨q為真命題,p∧q為假命題,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com