
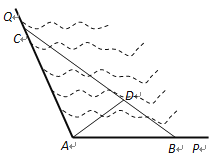
【題目】如圖所示,![]() 是某海灣旅游區的一角,其中
是某海灣旅游區的一角,其中![]() ,為了營造更加優美的旅游環境,旅游區管委會決定在直線海岸
,為了營造更加優美的旅游環境,旅游區管委會決定在直線海岸![]() 和
和![]() 上分別修建觀光長廊
上分別修建觀光長廊![]() 和AC,其中
和AC,其中![]() 是寬長廊,造價是
是寬長廊,造價是![]() 元/米,
元/米,![]() 是窄長廊,造價是
是窄長廊,造價是![]() 元/米,兩段長廊的總造價為120萬元,同時在線段
元/米,兩段長廊的總造價為120萬元,同時在線段![]() 上靠近點
上靠近點![]() 的三等分點
的三等分點![]() 處建一個觀光平臺,并建水上直線通道
處建一個觀光平臺,并建水上直線通道![]() (平臺大小忽略不計),水上通道的造價是
(平臺大小忽略不計),水上通道的造價是![]() 元/米.
元/米.
(1) 若規劃在三角形![]() 區域內開發水上游樂項目,要求
區域內開發水上游樂項目,要求![]() 的面積最大,那么
的面積最大,那么![]() 和
和![]() 的長度分別為多少米?
的長度分別為多少米?
(2) 在(1)的條件下,建直線通道![]() 還需要多少錢?
還需要多少錢?
【答案】(1)![]() 和AC的長度分別為750米和1500米(2)
和AC的長度分別為750米和1500米(2)![]() 萬元
萬元
【解析】
試題(1)設![]() 長為
長為![]() 米,
米,![]() 長為
長為![]() 米,依題意得
米,依題意得![]() ,即
,即![]() ,表示面積,利用基本不等式可得結論;(2)利用向量方法,將
,表示面積,利用基本不等式可得結論;(2)利用向量方法,將![]() 表示為
表示為![]() ,根據向量的數量積與模長的關系可得結果.
,根據向量的數量積與模長的關系可得結果.
試題解析:(1)設![]() 長為
長為![]() 米,
米,![]() 長為
長為![]() 米,依題意得
米,依題意得![]() ,
,
即![]() ,
,
![]()
![]()
![]()
![]() =
=![]()
![]()
當且僅當![]() ,即
,即![]() 時等號成立,
時等號成立,
所以當![]() 的面積最大時,
的面積最大時,![]() 和AC的長度分別為750米和1500米
和AC的長度分別為750米和1500米
(2)在(1)的條件下,因為![]() .
.
由![]()
得![]()
![]()
![]()
![]()
![]() ,
,
![]() 元
元
所以,建水上通道![]() 還需要
還需要![]() 萬元.
萬元.
解法二:在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,![]()
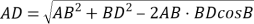
![]()
在![]() 中,
中,![]()
![]() =
=![]()
![]() 元
元
所以,建水上通道![]() 還需要
還需要![]() 萬元.
萬元.
解法三:以A為原點,以AB為![]() 軸建立平面直角坐標系,則
軸建立平面直角坐標系,則![]() ,
,![]()
![]() ,即
,即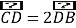 ,設
,設![]()
由![]() ,求得
,求得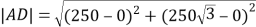 , 所以
, 所以![]()
所以,![]()
![]()
![]() 元
元
所以,建水上通道![]() 還需要
還需要![]() 萬元.
萬元.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】垃圾分一分,城市美十分;垃圾分類,人人有責.某市為進一步推進生活垃圾分類工作,調動全民參與的積極性,舉辦了“垃圾分類游戲挑戰賽”.據統計,在為期![]() 個月的活動中,共有
個月的活動中,共有![]() 萬人次參與.為鼓勵市民積極參與活動,市文明辦隨機抽取
萬人次參與.為鼓勵市民積極參與活動,市文明辦隨機抽取![]() 名參與該活動的網友,以他們單次游戲得分作為樣本進行分析,由此得到如下頻數分布表:
名參與該活動的網友,以他們單次游戲得分作為樣本進行分析,由此得到如下頻數分布表:
單次游戲得分 |
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
(1)根據數據,估計參與活動的網友單次游戲得分的平均值及標準差(同一組中的數據用該組區間的中點值作代表);(其中標準差的計算結果要求精確到![]() )
)
(2)若要從單次游戲得分在![]() 、
、![]() 、
、![]() 的三組參與者中,用分層抽樣的方法選取
的三組參與者中,用分層抽樣的方法選取![]() 人進行電話回訪,再從這
人進行電話回訪,再從這![]() 人中任選
人中任選![]() 人贈送話費,求此
人贈送話費,求此![]() 人單次游戲得分不在同一組內的概率.
人單次游戲得分不在同一組內的概率.
附:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為配合“2019雙十二”促銷活動,某公司的四個商品派送點如圖環形分布,并且公司給![]() 四個派送點準備某種商品各50個.根據平臺數據中心統計發現,需要將發送給
四個派送點準備某種商品各50個.根據平臺數據中心統計發現,需要將發送給![]() 四個派送點的商品數調整為40,45,54,61,但調整只能在相鄰派送點進行,每次調動可以調整1件商品.為完成調整,則( )
四個派送點的商品數調整為40,45,54,61,但調整只能在相鄰派送點進行,每次調動可以調整1件商品.為完成調整,則( )

A.最少需要16次調動,有2種可行方案
B.最少需要15次調動,有1種可行方案
C.最少需要16次調動,有1種可行方案
D.最少需要15次調動,有2種可行方案
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市對城市路網進行改造,擬在原有a個標段(注:一個標段是指一定長度的機動車道)的基礎上,新建x個標段和n個道路交叉口,其中n與x滿足n=ax+5.已知新建一個標段的造價為m萬元,新建一個道路交叉口的造價是新建一個標段的造價的k倍.
(1)寫出新建道路交叉口的總造價y(萬元)與x的函數關系式;
(2)設P是新建標段的總造價與新建道路交叉口的總造價之比.若新建的標段數是原有標段數的20%,且k≥3.問:P能否大于![]() ,說明理由.
,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在等腰梯形![]() 中,兩腰
中,兩腰![]() ,底邊
,底邊![]() 是
是![]() 的三等分點,
的三等分點,![]() 是
是![]() 的中點.分別沿
的中點.分別沿![]() 將四邊形
將四邊形![]() 和
和![]() 折起,使
折起,使![]() 重合于點
重合于點![]() ,得到如圖2所示的幾何體.在圖2中,
,得到如圖2所示的幾何體.在圖2中,![]() 分別為
分別為![]() 的中點.
的中點.
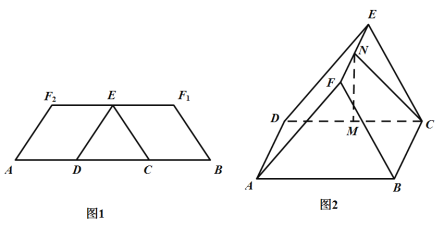
(1)證明:![]() 平面
平面![]()
(2)求幾何體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解貴州省某州2020屆高三理科生的化學成績的情況,該州教育局組織高三理科生進行了摸底考試,現從參加考試的學生中隨機抽取了100名理科生,,將他們的化學成績(滿分為100分)分為![]()
![]()
![]()
![]()
![]()
![]() 6組,得到如圖所示的頻率分布直方圖.
6組,得到如圖所示的頻率分布直方圖.

(1)求a的值;
(2)記A表示事件“從參加考試的所有理科生中隨機抽取一名學生,該學生的化學成績不低于70分”,試估計事件A發生的概率;
(3)在抽取的100名理科生中,采用分層抽樣的方法從成績在![]() 內的學生中抽取10名,再從這10名學生中隨機抽取4名,記這4名理科生成績在
內的學生中抽取10名,再從這10名學生中隨機抽取4名,記這4名理科生成績在![]() 內的人數為X,求X的分布列與數學期望.
內的人數為X,求X的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是各項均不為0的等差數列,公差為
是各項均不為0的等差數列,公差為![]() ,
,![]() 為其前
為其前![]() 項和,且滿足
項和,且滿足![]() .數列
.數列![]() 滿足
滿足![]() ,
,![]() 為數列
為數列![]() 的前
的前![]() 項和.
項和.
(1)求![]() ;
;
(2)求![]() ;
;
(3)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 過點
過點![]() ,左焦點
,左焦點![]()
(1)求橢圓C的標準方程;
(2)過點F作于x軸不重合的直線l,l與橢圓交于A,B兩點,點A在直線![]() 上的投影N與點B的連線交x軸于D點,D點的橫坐標
上的投影N與點B的連線交x軸于D點,D點的橫坐標![]() 是否為定值?若是,請求出定值;若不是,請說明理由
是否為定值?若是,請求出定值;若不是,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.

(I)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(II)若二面角P-CD-A的大小為45°,求直線PA與平面PCE所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com