【題目】在直角坐標系xOy中，曲線C的參數方程為
（α為參數），將C上每一點的橫坐標保持不變，縱坐標變為原來的3倍，得曲線C1．以O為極點，x軸正半軸為極軸建立極坐標系．
（1）求C1的極坐標方程
（2）設M，N為C1上兩點，若OM⊥ON，求
的值．
閱讀快車系列答案科目：高中數學 來源： 題型：
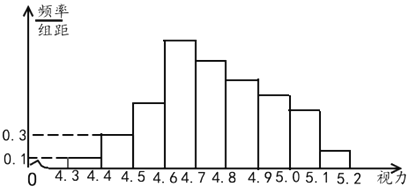
【題目】如圖是由容量為100的樣本得到的頻率分布直方圖．其中前4組的頻率成等比數列，后6組的頻數成等差數列，設最大頻率為a，在
到
之間的數據個數為b，則a，b的值分別為（ ）
A.
，78
B.，83
C.
，78
D.，83
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c.滿足2acosC+bcosC+ccosB=0.
(Ⅰ)求角C的大小；
(Ⅱ)若a=2,△ABC的面積為
，求C的大小。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為拋物線
：
的焦點，過的動直線交拋物線于
，
兩點．當直線與
軸垂直時，
．
（1）求拋物線的方程；
（2）設直線
的斜率為1且與拋物線的準線
相交于點
，拋物線上存在點
使得直線
，
，
的斜率成等差數列，求點的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“新車嗨翻天!首付3000元起開新車”這就是毛豆新車網打出來的廣告語．某人看到廣告，興奮不已，計劃于2019年1月在該網站購買一輛某品牌汽車，他從當地了解到近五個月該品牌汽車實際銷量如表：
月份 | 2018.08 | 2018.09 | 2018.10 | 2018.11 | 2018.12 |
月份編號t | 1 | 2 | 3 | 4 | 5 |
銷量y（萬輛） | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
（1）經分析，可用線性回歸模型擬合當地該品牌汽車實際銷量y（萬輛）與月份編號t之間的相關關系．請用最小二乘法求y關于t的線性回歸方程
，并估計2019年1月份該品牌汽車的銷量：
（2）為了增加銷量，廠家和毛豆新車網聯合推出對購該品牌車進行補貼．已知某地擬購買該品牌汽車的消費群體十分龐大，某調研機構對其中的200名消費者的購車補貼金額的心理預期值進行了一個抽樣調查，得到如下一份頻數表：
補貼金額預期值 區間（萬元） | [1，2） | [2，3） | [3，4） | [4，5） | [5，6） | [6，7） |
頻數 | 20 | 60 | 60 | 30 | 20 | 10 |
將頻率視為概率，現用隨機抽樣方法從該地區擬購買該品牌汽車的所有消費者中隨機抽取3人，記被抽取3人中對補貼金額的心理預期值不低于3萬元的人數為ξ，求ξ的分布列及數學期望E（ξ）
參考公式及數據：①回歸方程
，其中
，
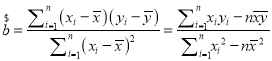；②
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
的離心率為2，左右焦點分別為
，
，過右焦點且垂直于x軸的直線與雙曲線交于A，B兩點，且
的周長為
．
（1）求雙曲線C的方程；
（2）已知直線
，點P是雙曲線C上的動點，求點P到直線l的距離的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線l：
與橢圓
交于A，B兩點，點P是橢圓C上異于A，B的一個動點，點Q在直線AB上，滿足
(
為坐標原點)
（1）求點Q的軌跡方程；
（2）求四邊形OAPB的面積S的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，以坐標原點為極點，
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
為曲線上的動點，點
在射線
上，且滿足
.
（Ⅰ）求點的軌跡
的直角坐標方程；
（Ⅱ）設與軸交于點
，過點且傾斜角為
的直線
與相交于
兩點，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，以原點
為圓心，橢圓
的長軸為直徑的圓與直線
相切.
（1）求橢圓的標準方程；
（2）已知過點
的動直線與橢圓的兩個交點為
，求
的面積S的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
