
【題目】已知函數f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π),其圖象最低點的縱坐標是-![]() ,相鄰的兩個對稱中心是(
,相鄰的兩個對稱中心是(![]() ,0)和(
,0)和(![]() ,0).求:
,0).求:
(1)f(x)的解析式;
(2)f(x)的值域;
(3)f(x)圖象的對稱軸.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】下列命題中正確的個數是( )
①如果![]() 、
、![]() 是兩條直線,
是兩條直線,![]() ,那么
,那么![]() 平行于過
平行于過![]() 的任何一個平面;②如果直線
的任何一個平面;②如果直線![]() 滿足
滿足![]() ,那么
,那么![]() 與平面
與平面![]() 內的任何一條直線平行;③如果直線
內的任何一條直線平行;③如果直線![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,則
,則![]() ;④如果直線
;④如果直線![]() 、
、![]() 和平面
和平面![]() 滿足
滿足![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;⑤如果
;⑤如果![]() 與平面
與平面![]() 內的無數條直線平行,那么直線
內的無數條直線平行,那么直線![]() 必平行于平面
必平行于平面![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的一系列對應值如下表:
的一系列對應值如下表:

(1)根據表格提供的數據求出函數![]() 的一個解析式;
的一個解析式;
(2)根據(1)的結果,若函數![]() 的周期為
的周期為![]() ,當
,當![]() 時,方程
時,方程![]() 恰有兩個不同的解,求實數
恰有兩個不同的解,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(10分)若集合A={x|x2+5x﹣6=0},B={x|x2+2(m+1)x+m2﹣3=0}.
(1)若m=0,寫出A∪B的子集;
(2)若A∩B=B,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() ,若已知其在
,若已知其在![]() 內只取到一個最大值和一個最小值,且當
內只取到一個最大值和一個最小值,且當![]() 時函數取得最大值為
時函數取得最大值為![]() ;當
;當![]() ,函數取得最小值為
,函數取得最小值為![]() .
.
(1)求出此函數的解析式;
(2)是否存在實數![]() ,滿足不等式
,滿足不等式![]() ?若存在,求出
?若存在,求出![]() 的范圍(或值),若不存在,請說明理由;
的范圍(或值),若不存在,請說明理由;
(3)若將函數![]() 的圖像保持橫坐標不變縱坐標變為原來的
的圖像保持橫坐標不變縱坐標變為原來的![]() 得到函數
得到函數![]() ,再將函數
,再將函數![]() 的圖像向左平移
的圖像向左平移![]() 個單位得到函數
個單位得到函數![]() ,已知函數
,已知函數![]() 的最大值為
的最大值為![]() ,求滿足條件的
,求滿足條件的![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某群體的人均通勤時間,是指單日內該群體中成員從居住地到工作地的平均用時,某地上班族![]() 中的成員僅以自駕或公交方式通勤,分析顯示:當
中的成員僅以自駕或公交方式通勤,分析顯示:當![]() 中
中![]() 的成員自駕時,自駕群體的人均通勤時間為
的成員自駕時,自駕群體的人均通勤時間為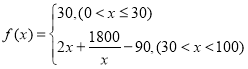 (單位:分鐘),而公交群體的人均通勤時間不受
(單位:分鐘),而公交群體的人均通勤時間不受![]() 影響,恒為40分鐘,試根據上述分析結果回答下列問題:
影響,恒為40分鐘,試根據上述分析結果回答下列問題:
(1)當![]() 在什么范圍內時,公交群體的人均通勤時間少于自駕群體的人均通勤時間?
在什么范圍內時,公交群體的人均通勤時間少于自駕群體的人均通勤時間?
(2)求該地上班族![]() 的人均通勤時間
的人均通勤時間![]() 的表達式;并求
的表達式;并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種計算機病毒是通過電子郵件進行傳播的,下表是某公司前5天監測到的數據:
第 | 1 | 2 | 3 | 4 | 5 |
被感染的計算機數量 | 10 | 20 | 39 | 81 | 160 |
則下列函數模型中,能較好地反映計算機在第![]() 天被感染的數量
天被感染的數量![]() 與
與![]() 之間的關系的是
之間的關系的是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com