
【題目】數列![]() 為遞增的等比數列,
為遞增的等比數列, ![]()
![]() ,
,
數列![]() 滿足
滿足![]() .
.
(Ⅰ)求數列![]() 的通項公式;(Ⅱ)求證:
的通項公式;(Ⅱ)求證: ![]() 是等差數列;
是等差數列;
(Ⅲ)設數列![]() 滿足
滿足![]() ,且數列
,且數列![]() 的前
的前![]() 項和
項和![]() ,并求使得
,并求使得![]() 對任意
對任意![]() 都成立的正整數
都成立的正整數![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]() 是首項為1,公差為2的等差數列. (3)4
是首項為1,公差為2的等差數列. (3)4
【解析】試題分析:(1)根據{an}為遞增的等比數列且a32=a1a5,得到a1=1,a3=4,a5=16,進而求得an,bn的通項公式;(2)利用等差數列定義加以證明;(3)利用裂項相消法求數列的前n項和,再用分離參數法和單調性求m的最小值.
試題解析:
(1)數列![]() 為遞增的等比數列,則其公比為正數,又
為遞增的等比數列,則其公比為正數,又![]() ,當且僅當
,當且僅當![]() 時成立。此時公比
時成立。此時公比![]() 所以
所以![]() .
.
(2) 因為 ![]() ,所以
,所以![]() ,即
,即![]() .
.
所以![]() 是首項為
是首項為![]() ,公差為2的等差數列.
,公差為2的等差數列.
(3)![]() ,所以
,所以![]() .
.
![]() ,
,
![]()
![]() ,n∈N*,即數列{Tn}是遞增數列.∴當n=1時,Tn取得最小值
,n∈N*,即數列{Tn}是遞增數列.∴當n=1時,Tn取得最小值![]() ,
,
要使得![]() 對任意n∈N*都成立,結合(Ⅰ)的結果,只需
對任意n∈N*都成立,結合(Ⅰ)的結果,只需![]() ,
,
![]() ,故正整數m的最小值為4.
,故正整數m的最小值為4.


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知函數是定義在![]() ,
, ![]() ,
, ![]() 上的奇函數,當
上的奇函數,當![]() ,
, ![]() 時,
時, ![]() (
(![]() ).
).
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)設![]() ,
, ![]() ,
, ![]() ,求證:當
,求證:當![]() 時,
時, ![]() 恒成立;
恒成立;
(Ⅲ)是否存在實數![]() ,使得當
,使得當![]() ,
, ![]() 時,
時, ![]() 的最小值是
的最小值是![]() ?如果存在,
?如果存在,
求出實數![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著我國經濟的快速發展,民用汽車的保有量也迅速增長.機動車保有量的發展影響到環境質量、交通安全、道路建設等諸多方面.在我國,尤其是大中型城市,機動車已成為城市空氣污染的重要來源.因此,合理預測機動車保有量是未來進行機動車污染防治規劃、道路發展規劃等的重要前提.從2012年到2016年,根據“云南省某市國民經濟和社會發展統計公報”中公布的數據,該市機動車保有量數據如表所示.
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代碼 | 1 | 2 | 3 | 4 | 5 |
機動車保有量 | 169 | 181 | 196 | 215 | 230 |
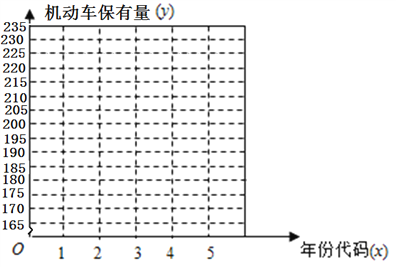
(1)在圖所給的坐標系中作出數據對應的散點圖;
(2)建立機動車保有量![]() 關于年份代碼
關于年份代碼![]() 的回歸方程;
的回歸方程;
(3)按照當前的變化趨勢,預測2017年該市機動車保有量.
附注:回歸直線方程![]() 中的斜率和截距的最小二乘估計公式分別為:
中的斜率和截距的最小二乘估計公式分別為:
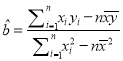 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工廠從今年一月起,若不改善生產環境,按生產現狀,每月收入為70萬元,同時將受到環保部門的處罰,第一個月罰3萬元,以后每月增加2萬元.如果從今年一月起投資500萬元添加回收凈化設備(改造設備時間不計),一方面可以改善環境,另一方面也可以大大降低原料成本.據測算,添加回收凈化設備并投產后的前5個月中的累計生產凈收入![]() 是生產時間
是生產時間![]() 個月的二次函數
個月的二次函數![]() (
(![]() 是常數),且前3個月的累計生產凈收入可達309萬,從第6個月開始,每個月的生產凈收入都與第5個月相同.同時,該廠不但不受處罰,而且還將得到環保部門的一次性獎勵100萬元.
是常數),且前3個月的累計生產凈收入可達309萬,從第6個月開始,每個月的生產凈收入都與第5個月相同.同時,該廠不但不受處罰,而且還將得到環保部門的一次性獎勵100萬元.
(1)求前8個月的累計生產凈收入![]() 的值;
的值;
(2)問經過多少個月,投資開始見效,即投資改造后的純收入多于不改造時的純收入.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某運動員每次投籃命中的概率都為40%,現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中;5,6,7,8,9,0表示不命中;再以每三個隨機數為一組,代表三次投籃的結果,經隨機模擬產生了如下20組隨機數,據此估計,該運動員三次投籃恰有兩次命中的概率為( )
137 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
A.0.40 B.0.30 C.0.35 D.0.25
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 中,M,N分別為
中,M,N分別為![]() 的中點.
的中點.
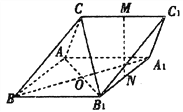
(1)證明:直線MN//平面CAB1;
(2)若四邊形ABB1A1是菱形,且![]() ,
, ![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角(銳角)的余弦值.
所成的角(銳角)的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com