
【題目】(1)求經(jīng)過直線l1:2x+3y-5=0與l2:7x+15y+1=0的交點(diǎn),且平行于直線x+2y-3=0的直線方程;
(2)求與直線3x+4y-7=0垂直,且與原點(diǎn)的距離為6的直線方程.
【答案】(1)9x+18y-4=0(2)4x-3y±30=0.
【解析】
試題分析:(1)聯(lián)立![]() ,解得交點(diǎn)P的坐標(biāo).設(shè)平行于直線 x+2y-3=0的直線方程為 x+2y+n=0.代入即可得出;(2)設(shè)與直線3x+4y-7=0垂直的直線方程為:4x-3y+m=0.又與原點(diǎn)的距離為6,可得
,解得交點(diǎn)P的坐標(biāo).設(shè)平行于直線 x+2y-3=0的直線方程為 x+2y+n=0.代入即可得出;(2)設(shè)與直線3x+4y-7=0垂直的直線方程為:4x-3y+m=0.又與原點(diǎn)的距離為6,可得 ,解得m即可.
,解得m即可.
試題解析:(1)設(shè)所求的直線方程為2x+3y-5+λ(7x+15y+1)=0,
即(2+7λ)x+(3+15λ)y+λ-5=0,由已知-![]() =-
=-![]() ,解得λ=1.
,解得λ=1.
故所求的直線方程為9x+18y-4=0.
(2)設(shè)所求的直線方程為4x-3y+c=0.由已知:![]() =6,解得c=±30,
=6,解得c=±30,
故所求的直線方程為4x-3y±30=0.


 奪冠訓(xùn)練單元期末沖刺100分系列答案
奪冠訓(xùn)練單元期末沖刺100分系列答案 新思維小冠軍100分作業(yè)本系列答案
新思維小冠軍100分作業(yè)本系列答案 名師指導(dǎo)一卷通系列答案
名師指導(dǎo)一卷通系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() (
(![]() ).
).
(1)當(dāng)![]() 時,求
時,求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() ,
,![]() 存在兩個極值點(diǎn)
存在兩個極值點(diǎn)![]() ,
,![]() ,試比較
,試比較![]() 與
與![]() 的大小;
的大小;
(3)求證:![]() (
(![]() ,
,![]() ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】經(jīng)市場調(diào)查:生產(chǎn)某產(chǎn)品需投入年固定成本為3萬元,每生產(chǎn)![]() 萬件,需另投入流動成本為
萬件,需另投入流動成本為![]() 萬元,在年產(chǎn)量不足8萬件時,
萬元,在年產(chǎn)量不足8萬件時,![]()
![]() (萬元),在年產(chǎn)量不小于8萬件時,
(萬元),在年產(chǎn)量不小于8萬件時,![]() (萬元).通過市場分析,每件產(chǎn)品售價為5元時,生產(chǎn)的商品能當(dāng)年全部售完.
(萬元).通過市場分析,每件產(chǎn)品售價為5元時,生產(chǎn)的商品能當(dāng)年全部售完.
(1)寫出年利潤![]() (萬元)關(guān)于年產(chǎn)量
(萬元)關(guān)于年產(chǎn)量![]() (萬件)的函數(shù)解析式;
(萬件)的函數(shù)解析式;
(2)寫出當(dāng)產(chǎn)量為多少時利潤最大,并求出最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列條件中,能使直線m⊥平面α的是( )
A.m⊥b,m⊥c,bα,cα
B.m⊥b,b∥α
C.m∩b=A,b⊥α
D.m∥b,b⊥α
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某單位有840名職工,現(xiàn)采用系統(tǒng)抽樣方法,抽取42人做問卷調(diào)查,將840人按1,2,…,840隨機(jī)編號,則抽取的42人中,編號落入?yún)^(qū)間[481,720]的人數(shù)為 ( )
A. 11 B. 12
C. 13 D. 14
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在對人們的休閑方式的一次調(diào)查中,共調(diào)查了![]() 人,其中女性
人,其中女性![]() 人,男性
人,男性![]() 人.女性中有
人.女性中有![]() 人主要的休閑方式是看電視,另外
人主要的休閑方式是看電視,另外![]() 人主要的休閑方式是運(yùn)動;男性中有
人主要的休閑方式是運(yùn)動;男性中有![]() 人主要的休閑方式是看電視,另外
人主要的休閑方式是看電視,另外![]() 人主要的休閑方式是運(yùn)動.
人主要的休閑方式是運(yùn)動.
(1)根據(jù)以上數(shù)據(jù)建立一個2×2的列聯(lián)表;
(2)是否有97.5%的把握認(rèn)為性別與休閑方式有關(guān)系?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知y=f(x),x∈(-a,a),F(xiàn)(x)=f(x)+f(-x),則F(x)是( )
A.奇函數(shù)
B.偶函數(shù)
C.既是奇函數(shù)又是偶函數(shù)
D.非奇非偶函數(shù)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
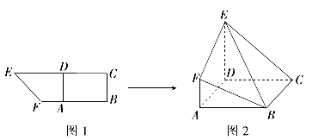
【題目】如圖所示,在直角梯形![]() 中,
中,![]() ,
,![]() 分別是
分別是![]() 上的點(diǎn),
上的點(diǎn),![]() ,且
,且![]() (如圖1). 將四邊形
(如圖1). 將四邊形![]() 沿
沿![]() 折起,連結(jié)
折起,連結(jié)![]() (如圖2). 在折起的過程中,下列說法中錯誤的個數(shù)是( )
(如圖2). 在折起的過程中,下列說法中錯誤的個數(shù)是( )
①![]() 平面
平面![]() ;
;
②![]() 四點(diǎn)不可能共面;
四點(diǎn)不可能共面;
③若![]() ,則平面
,則平面![]() 平面
平面![]() ;
;
④平面![]() 與平面
與平面![]() 可能垂直.
可能垂直.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com