【題目】已知橢圓
＋
＝1(a>b>0)上的點P到左，右兩焦點F1，F2的距離之和為2
，離心率為
.
(1)求橢圓的標(biāo)準(zhǔn)方程；
(2)過右焦點F2的直線l交橢圓于A，B兩點，若y軸上一點M(0，
)滿足|MA|＝|MB|，求直線l的斜率k的值．
【答案】（1）
；（2）
．
【解析】
試題分析：（1）根據(jù)
與離心率可求得a，b，c的值，從而就得到橢圓的方程；（2）設(shè)出直線的方程
，并與橢圓方程聯(lián)立消去y可得到關(guān)于x的一元二次方程，然后利用中點坐標(biāo)公式與分類討論的思想進(jìn)行解決．
試題解析：（1）
，∴
，
，∴
，∴
，
橢圓的標(biāo)準(zhǔn)方程為．
（2）已知
,設(shè)直線的方程為，
-，
聯(lián)立直線與橢圓的方程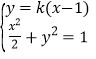
，化簡得：
，
∴
，
，
∴
的中點坐標(biāo)為
．
①當(dāng)
時，的中垂線方程為
，
∵
，∴點
在的中垂線上，將點的坐標(biāo)代入直線方程得：
，即
，
解得
或
．
②當(dāng)
時，的中垂線方程為
，滿足題意，
∴斜率
的取值為.
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知圓O的內(nèi)接四邊形BCED，BC為圓O的直徑，BC=2，延長CB，ED交于A點，使得∠DOB=∠ECA，過A作圓O的切線，切點為P，
（1）求證：BD=DE；
（2）若∠ECA=45°，求AP2的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知正項等差數(shù)列{an}的前n項和為Sn ， 且滿足 
，S7=56．
（1）求數(shù)列{an}的通項公式an；
（2）若數(shù)列{bn}滿足b1=a1且bn+1﹣bn=an+1 ， 求數(shù)列 
的前n項和Tn ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在四棱錐B﹣ACDE中，AE⊥平面ABC，CD∥AE，∠ABC=3∠BAC=90°，BF⊥AC于F，AC=4CD=4，AE=3．
（1）求證：BE⊥DF；
（2）求二面角B﹣DE﹣F的平面角的余弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知雙曲線的頂點與焦點分別是橢圓
的焦點與頂點，若雙曲線的兩條漸近線與橢圓的交點構(gòu)成的四邊形恰為正方形，則橢圓的離心率為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)列{an}（n=1，2，3，…）滿足an+1=2an ， 且a1 ， a2+1，a3成等差數(shù)列，設(shè)bn=3log2an﹣7．
（1）求數(shù)列{an}，{bn}的通項公式；
（2）求數(shù)列{|bn|}的前n項和Tn ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知關(guān)于x的一次函數(shù)
．
（Ⅰ）設(shè)集合
和
，分別從集合
和
中隨機(jī)取一個數(shù)作為m和n，求函數(shù)是增函數(shù)的概率；
（Ⅱ）實數(shù)m，n滿足條件
求函數(shù)的圖象經(jīng)過一、二、三象限的概率．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
