【題目】如圖，等邊△ABC與直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M為AB的中點．
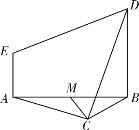
(1)證明：CM⊥DE；
(2)在邊AC上找一點N，使CD∥平面BEN.
【答案】（1）見解析；（2）
為
邊上靠近
的三等分點；證明見解析.
【解析】
（1）根據等邊三角形證得
，再根據面面垂直的性質定理得到線面垂直，利用線面垂直的性質得到結論；（2）取面
，當
與上一點連線構成平面時，根據線面平行性質定理可知：所得平面與面的交線必平行于
；兩面已有一個交點
，則只需過作的平行線，與交點即為，根據長度關系可知：為邊上靠近的三等分點；通過找
中點
得
，易證得
為
和
中點；根據平行線分線段成比例和長度關系可證得
，從而證得
，再利用三角形中位線得
，從而有
，根據線面平行判定定理，可證得結論成立.
（1）
為等邊三角形，且
為
中點 
又平面
平面
，平面
平面
，
平面
平面
又
平面 
（2）為邊上靠近的三等分點，證明如下：
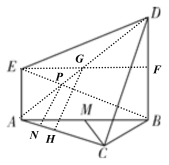
取中點，連接交于
取中點
，連接；連接
交于
，為中點，
為中點
為邊上靠近的三等分點
即
即
又
分別為
中點 
又
面
，
面 
面
優學名師名題系列答案科目：高中數學 來源： 題型：
【題目】已知函數f (x)＝ex，g(x)＝x－b，b∈R．
（1）若函數f (x)的圖象與函數g(x)的圖象相切，求b的值；
（2）設T(x)＝f (x)＋ag(x)，a∈R，求函數T(x)的單調增區間；
（3）設h(x)＝|g(x)|·f (x)，b＜1．若存在x1，x2
[0，1]，使|h(x1)－h(x2)|＞1成立，求b的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給定橢圓C：
(a＞b＞0)，稱圓C1：x2＋y2＝a2＋b2為橢圓C的“伴隨圓”．已知橢圓C的離心率為
，且經過點(0，1)．
（1）求實數a，b的值；
（2）若過點P(0，m)(m＞0)的直線l與橢圓C有且只有一個公共點，且l被橢圓C的伴隨圓C1所截得的弦長為2
，求實數m的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙、丙3人投籃,投進的概率分別是
.
(Ⅰ)現3人各投籃1次,求3人都沒有投進的概率；
(Ⅱ)用
表示乙投籃3次的進球數,求隨機變量的概率分布及數學期望
；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】交通指數是指交通擁堵指數的簡稱，是綜合反映道路網暢通或擁堵的概念性指數值，記交通指數為
，其范圍為
，分別有五個級別：
，暢通；
，基本暢通；
，輕度擁堵；
，中度擁堵；
，嚴重擁堵.在晚高峰時段（
），從某市交通指揮中心選取了市區20個交通路段，依據其交通指數數據繪制的頻率分布直方圖如圖所示.
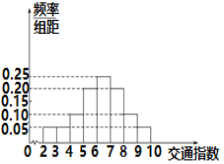
(1)求出輕度擁堵、中度擁堵、嚴重擁堵的路段的個數；
(2)用分層抽樣的方法從輕度擁堵、中度擁堵、嚴重擁堵的路段中共抽取6個路段，求依次抽取的三個級別路段的個數；
(3)從(2)中抽取的6個路段中任取2個，求至少有1個路段為輕度擁堵的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區100位居民的人均月用水量(單位：
)的分組及各組的頻數如下：
，4； 
，8； 
，15；
，22； 
，25； 
，14；
，6； 
，4； 
，2．
(1)列出樣本的頻率分布表；
(2)畫出頻率分布直方圖，并根據直方圖估計這組數據的平均數、中位數、眾數；
(3)當地政府制定了人均月用水量為
的標準，若超出標準加倍收費，當地政府說，
以上的居民不超過這個標準，這個解釋對嗎？為什么？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
