
【題目】在平面直角坐標系xOy中,過點 的圓的圓心C在x軸上,且與過原點傾斜角為30°的直線l相切.
的圓的圓心C在x軸上,且與過原點傾斜角為30°的直線l相切.
(1)求圓C的標準方程;
(2)求直線![]() 被圓C截得的弦長;
被圓C截得的弦長;
(3)點P在直線m:![]() 上,過點P作⊙C的切線PM、PN,切點分別為M、N,求經過P、M、N、C四點的圓所過的定點坐標.
上,過點P作⊙C的切線PM、PN,切點分別為M、N,求經過P、M、N、C四點的圓所過的定點坐標.
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,過點
,過點![]() 的直線與拋物線
的直線與拋物線![]() 相切,設第一象限的切點為
相切,設第一象限的切點為![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)若過點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 相交于兩點
相交于兩點![]() ,圓
,圓![]() 是以線段
是以線段![]() 為直徑的圓過點
為直徑的圓過點![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小電子產品2018年的價格為9元/件,年銷量為![]() 件,經銷商計劃在2019年將該電子產品的價格降為
件,經銷商計劃在2019年將該電子產品的價格降為![]() 元/件(其中
元/件(其中![]() ),經調查,顧客的期望價格為5元/件,經測算,該電子產品的價格下降后年銷量新增加了
),經調查,顧客的期望價格為5元/件,經測算,該電子產品的價格下降后年銷量新增加了![]() 件(其中常數
件(其中常數![]() ).已知該電子產品的成本價格為4元/件.
).已知該電子產品的成本價格為4元/件.
(1)寫出該電子產品價格下降后,經銷商的年收益![]() 與實際價格
與實際價格![]() 的函數關系式:(年收益=年銷售收入-成本)
的函數關系式:(年收益=年銷售收入-成本)
(2)設![]() ,當實際價格最低定為多少時,仍然可以保證經銷商2019年的收益比2018年至少增長20%?
,當實際價格最低定為多少時,仍然可以保證經銷商2019年的收益比2018年至少增長20%?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別為內角A,B,C的對邊,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面積S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:y=![]() x+4,動圓⊙O:x2+y2=r2(1<r<2),菱形ABCD的一個內角為60°,頂點A、B在直線l上,頂點C、D在⊙O上.當r變化時,求菱形ABCD的面積S的取值范圍.
x+4,動圓⊙O:x2+y2=r2(1<r<2),菱形ABCD的一個內角為60°,頂點A、B在直線l上,頂點C、D在⊙O上.當r變化時,求菱形ABCD的面積S的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某輛汽車以![]() 千米
千米![]() 小時的速度在高速公路上勻速行駛(考慮到高速公路行車安全要求
小時的速度在高速公路上勻速行駛(考慮到高速公路行車安全要求![]() 時,每小時的油耗(所需要的汽油量)為
時,每小時的油耗(所需要的汽油量)為![]() 升,其中
升,其中![]() 為常數,且
為常數,且![]() .
.
(1)若汽車以120千米![]() 小時的速度行駛時,每小時的油耗為11.5升,欲使每小時的油耗不超過9升,求
小時的速度行駛時,每小時的油耗為11.5升,欲使每小時的油耗不超過9升,求![]() 的取值范圍;
的取值范圍;
(2)求該汽車行駛100千米的油耗的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,(
,(![]() ,
,![]() ,
,![]() )的部分圖像如圖所示.
)的部分圖像如圖所示.
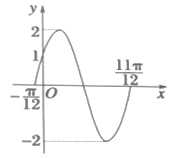
(1)求函數![]() 的解析式及
的解析式及![]() 圖像的對稱軸方程;
圖像的對稱軸方程;
(2)把函數![]() 圖像上點的橫坐標擴大到原來的2倍(縱坐標不變),再向左平移
圖像上點的橫坐標擴大到原來的2倍(縱坐標不變),再向左平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖象,求關于x的方程
的圖象,求關于x的方程![]() 在
在![]() 時所有的實數根之和.
時所有的實數根之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A(4,0)、B(1,0),動點M滿足|AM|=2|BM|.
(1)求動點M的軌跡C的方程;
(2)直線l:x+y=4,點N∈l,過N作軌跡C的切線,切點為T,求NT取最小時的切線方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com