
【題目】為了調查生活規律與患胃病是否與有關,某同學在當地隨機調查了200名30歲以上的人,并根據調查結果制成了不完整的列聯表如下:
不患胃病 | 患胃病 | 總計 | |
生活有規律 | 60 | 40 | |
生活無規律 | 60 | 100 | |
總計 | 100 |
(1)補全列聯表中的數據;
(2)用獨性檢驗的基本原理,說明生活無規律與患胃病有關時,出錯的概率不會超過多少?
參考公式和數表如下:
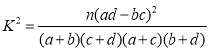
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|ax-2|,不等式f(x)≤4的解集為{x|-2≤x≤6}.
(1)求實數a的值;
(2)設g(x)=f(x)+f(x+3),若存在x∈R,使g(x)-tx≤2成立,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】科研人員在對人體脂肪含量和年齡之間關系的研究中,獲得了一些年齡和脂肪含量的簡單隨機樣本數據,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根據上表的數據得到如下的散點圖.
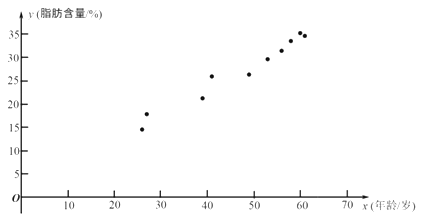
(1)根據上表中的樣本數據及其散點圖:
(i)求![]() ;
;
(i)計算樣本相關系數(精確到0.01),并刻畫它們的相關程度.
(2)若![]() 關于
關于![]() 的線性回歸方程為
的線性回歸方程為![]() ,求
,求![]() 的值(精確到0.01),并根據回歸方程估計年齡為50歲時人體的脂肪含量.
的值(精確到0.01),并根據回歸方程估計年齡為50歲時人體的脂肪含量.
附:參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
參考公式:相關系數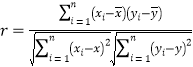
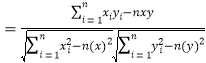
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為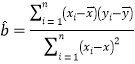 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年5月,來自“一帶一路”沿線的20國青年評選出了中國的“新四大發明”:高鐵、掃碼支付、共享單車和網購.乘坐高鐵可以網絡購票,為了研究網絡購票人群的年齡分布情況,在5月31日重慶到成都高鐵9600名網絡購票的乘客中隨機抽取了120人進行了統計并記錄,按年齡段將數據分成6組:![]() ,得到如圖所示的直方圖:
,得到如圖所示的直方圖:
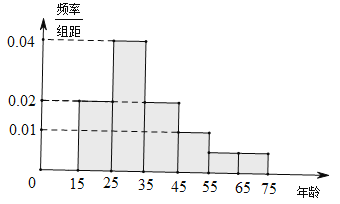
(1)若從總體的9600名網絡購票乘客中隨機抽取一人,估計其年齡大于35歲的概率;
(2)試估計總體中年齡在區間![]() 內的人數;
內的人數;
(3)試通過直方圖,估計5月31日當天網絡購票的9600名乘客年齡的中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農戶計劃種植萵筍和西紅柿,種植面積不超過![]() 畝,投入資金不超過
畝,投入資金不超過![]() 萬元,假設種植萵筍和西紅柿的產量、成本和售價如下表:
萬元,假設種植萵筍和西紅柿的產量、成本和售價如下表:
年產量/畝 | 年種植成本/畝 | 每噸售價 | |
萵筍 | 5噸 | 1萬元 | 0.5萬元 |
西紅柿 | 4.5噸 | 0.5萬元 | 0.4萬元 |
那么,該農戶一年種植總利潤(總利潤=總銷售收入-總種植成本)的最大值為____萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列說法:
(1)命題“![]() ,
,![]() ”的否定形式是“
”的否定形式是“![]() ,
,![]() ”;
”;
(2)已知![]() ,則
,則![]() ;
;
(3)已知回歸直線的斜率的估計值是2,樣本點的中心為![]() ,則回歸直線方程為
,則回歸直線方程為![]() ;
;
(4)對分類變量![]() 與
與![]() 的隨機變量
的隨機變量![]() 的觀測值
的觀測值![]() 來說,
來說,![]() 越小,判斷“
越小,判斷“![]() 與
與![]() 有關系”的把握越大;
有關系”的把握越大;
(5)若將一組樣本數據中的每個數據都加上同一個常數后,則樣本的方差不變.
其中正確說法的個數為( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為發展業務,某調研組對![]() ,
,![]() 兩個公司的產品需求量進行調研,準備從國內
兩個公司的產品需求量進行調研,準備從國內![]() 個人口超過
個人口超過![]() 萬的超大城市和
萬的超大城市和![]() (
(![]() )個人口低于
)個人口低于![]() 萬的小城市隨機抽取若干個進行統計,若一次抽取
萬的小城市隨機抽取若干個進行統計,若一次抽取![]() 個城市,全是小城市的概率為
個城市,全是小城市的概率為![]() .
.
(1)求![]() 的值;
的值;
(2)若一次抽取![]() 個城市,則:①假設取出小城市的個數為
個城市,則:①假設取出小城市的個數為![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
②若取出的![]() 個城市是同一類城市,求全為超大城市的概率.
個城市是同一類城市,求全為超大城市的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的普通方程與直線
的普通方程與直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓與拋物線![]() 有一個相同的焦點,且該橢圓的離心率為
有一個相同的焦點,且該橢圓的離心率為![]() ,
,
(Ⅰ)求該橢圓的標準方程:
(Ⅱ)求過點![]() 的直線與該橢圓交于A,B兩點,O為坐標原點,若
的直線與該橢圓交于A,B兩點,O為坐標原點,若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com