
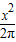 )2+(
)2+(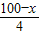 )2(0<x<100).
)2(0<x<100). -
- (100-x).
(100-x). (cm).
(cm).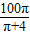 )內(nèi)單調(diào)遞減,在(
)內(nèi)單調(diào)遞減,在(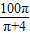 ,100)單調(diào)遞增
,100)單調(diào)遞增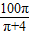 cm時,即彎成圓的一段長為
cm時,即彎成圓的一段長為 cm時,面積之和最小.
cm時,面積之和最小.

國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com