
【題目】已知過原點的動直線![]() 與圓
與圓![]()
![]() 相交于不同的兩點
相交于不同的兩點![]() .
.
(1)求圓![]() 的圓心坐標;
的圓心坐標;
(2)求線段![]() 的中點
的中點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)是否存在實數![]() ,使得直線
,使得直線![]()
![]() 與曲線
與曲線![]() 只有一個交點?若存在,求出
只有一個交點?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
【答案】(1)![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】
(1)將方程化為標準式方程,可得到圓心坐標;(2)設線段![]() 的中點,
的中點,![]() 直線
直線![]() 的方程為
的方程為![]() 聯立直線和圓的方程得到韋達定理,進而得到
聯立直線和圓的方程得到韋達定理,進而得到![]() ,
,![]() ,此時消去參數m即可得到軌跡方程;(3)結合第二問可得到曲線的軌跡,根據直線和圓的位置關系可得到滿足題意的結果.
,此時消去參數m即可得到軌跡方程;(3)結合第二問可得到曲線的軌跡,根據直線和圓的位置關系可得到滿足題意的結果.
(1)圓![]()
![]() 化為
化為![]() ,所以圓
,所以圓![]() 的圓心坐標為
的圓心坐標為![]()
(2)設線段![]() 的中點,
的中點,![]() 直線
直線![]() 的方程為
的方程為![]() (易知直線
(易知直線![]() 的斜率存在),則
的斜率存在),則![]() 得:
得:![]()
![]() .解得:
.解得:![]()
![]()
![]()
![]() 消去
消去![]() 得:
得:![]()
又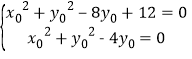 解得:
解得:![]() 或
或![]()
![]()
![]() 的軌跡
的軌跡![]() 的方程為
的方程為![]()
(3)由題意知直線![]() 表示過定點
表示過定點![]()
![]() ,斜率為
,斜率為![]() 的直線.
的直線.
![]() 表示的是一段關于
表示的是一段關于![]() 軸對稱,起點為
軸對稱,起點為![]() 按順時針方向運動到
按順時針方向運動到![]() 的圓弧(不包含端點
的圓弧(不包含端點![]() ).
).
由條件得:![]() 而當直線
而當直線![]() 與軌跡
與軌跡![]() 相切時,
相切時,![]() ,解得
,解得![]() (舍去).
(舍去).
可得當![]() 時,直線
時,直線![]() 與曲線
與曲線![]() 只有一個交點。
只有一個交點。
綜上所述,當時![]() 直線
直線![]()
![]() 與曲線
與曲線![]() 只有一個交點.
只有一個交點.


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系xOy中,曲線C1的參數方程為 ![]() (α為參數),將曲線C1上所有點的橫坐標縮短為原來的
(α為參數),將曲線C1上所有點的橫坐標縮短為原來的 ![]() ,縱坐標縮短為原來的
,縱坐標縮短為原來的 ![]() ,得到曲線C2 , 在以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,直線l的極坐標方程為4ρsin(θ+
,得到曲線C2 , 在以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,直線l的極坐標方程為4ρsin(θ+ ![]() )+
)+ ![]() =0.
=0.
(1)求曲線C2的極坐標方程及直線l與曲線C2交點的極坐標;
(2)設點P為曲線C1上的任意一點,求點P到直線l的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
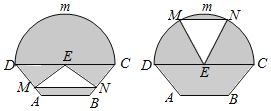
【題目】如圖所示的是自動通風設施![]() 該設施的下部ABCD是等腰梯形,其中
該設施的下部ABCD是等腰梯形,其中![]() 米,高
米,高![]() 米,
米,![]() 米
米![]() 上部CmD是個半圓,固定點E為CD的中點
上部CmD是個半圓,固定點E為CD的中點![]() 是由電腦控制其形狀變化的三角通風窗
是由電腦控制其形狀變化的三角通風窗![]() 陰影部分均不通風
陰影部分均不通風![]() ,MN是可以沿設施邊框上下滑動且始終保持和CD平行的伸縮橫桿.
,MN是可以沿設施邊框上下滑動且始終保持和CD平行的伸縮橫桿.
![]() 設MN與AB之間的距離為x米,試將三角通風窗
設MN與AB之間的距離為x米,試將三角通風窗![]() 的通風面積
的通風面積![]() 平方米
平方米![]() 表示成關于x的函數
表示成關于x的函數![]() ;
;
![]() 當MN與AB之間的距離為多少米時,三角通風窗
當MN與AB之間的距離為多少米時,三角通風窗![]() 的通風面積最大?求出這個最大面積.
的通風面積最大?求出這個最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
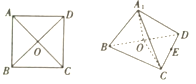
【題目】如圖,將邊長為2的正方體![]() 沿對角線
沿對角線![]() 折起,得到三棱錐
折起,得到三棱錐![]() ,則下列命題中,錯誤的為( )
,則下列命題中,錯誤的為( )
A. 直線![]() 平面
平面![]()
B. ![]()
C. 三棱錐![]() 的外接球的半徑為
的外接球的半徑為![]()
D. 若![]() 為
為![]() 的中點,則
的中點,則![]() 平面
平面![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】集合M={1,2…9}中抽取3個不同的數構成集合{a1 , a2 , a3}
(1)對任意i≠j,求滿足|ai﹣aj|≥2的概率;
(2)若a1 , a2 , a3成等差數列,設公差為ξ(ξ>0),求ξ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:極坐標與參數方程]
在直角坐標系xOy中,直線l的參數方程為 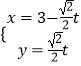 (t為參數).在極坐標系(與直角坐標系xOy取相同的長度單位),且以原點O為極點,以x軸正半軸為極軸)中,圓C的方程為ρ=4sinθ.
(t為參數).在極坐標系(與直角坐標系xOy取相同的長度單位),且以原點O為極點,以x軸正半軸為極軸)中,圓C的方程為ρ=4sinθ.
(1)求圓C的直角坐標方程和直線l普通方程;
(2)設圓C與直線l交于點A,B,若點P的坐標為(3,0),求|PA|+|PB|.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com