
【題目】為迎接2022年冬奧會,某市組織中學(xué)生開展冰雪運(yùn)動的培訓(xùn)活動,并在培訓(xùn)結(jié)束后對學(xué)生進(jìn)行了考核.記![]() 表示學(xué)生的考核成績,并規(guī)定
表示學(xué)生的考核成績,并規(guī)定![]() 為考核優(yōu)秀.為了了解本次培訓(xùn)活動的效果,在參加培訓(xùn)的學(xué)生中隨機(jī)抽取了30名學(xué)生的考核成績,并作成如圖所示的莖葉圖:
為考核優(yōu)秀.為了了解本次培訓(xùn)活動的效果,在參加培訓(xùn)的學(xué)生中隨機(jī)抽取了30名學(xué)生的考核成績,并作成如圖所示的莖葉圖:

(1)從參加培訓(xùn)的學(xué)生中隨機(jī)選取1人,請根據(jù)圖中數(shù)據(jù),估計這名學(xué)生考核為優(yōu)秀的概率;
(2)從圖中考核成績滿足![]() 的學(xué)生中任取3人,設(shè)
的學(xué)生中任取3人,設(shè)![]() 表示這3人中成績滿足
表示這3人中成績滿足![]() 的人數(shù),求
的人數(shù),求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(3)根據(jù)以往培訓(xùn)數(shù)據(jù),規(guī)定當(dāng)![]() 時培訓(xùn)有效.請你根據(jù)圖中數(shù)據(jù),判斷此次冰雪培訓(xùn)活動是否有效,并說明理由.
時培訓(xùn)有效.請你根據(jù)圖中數(shù)據(jù),判斷此次冰雪培訓(xùn)活動是否有效,并說明理由.
【答案】(1)![]() ;(2)分布列見解析,
;(2)分布列見解析,![]() ;(3)有效,理由見解析.
;(3)有效,理由見解析.
【解析】
(1) 由莖葉圖中的數(shù)據(jù)可以知道,30名同學(xué)中,有7名同學(xué)考核優(yōu)秀,則概率可求.
(2) ![]() 的所有可能取值為0,1,2,3,然后求出概率,列出分布列,計算期望.
的所有可能取值為0,1,2,3,然后求出概率,列出分布列,計算期望.
(3) 根據(jù)表格中的數(shù)據(jù),滿足![]() 的成績有16個,可求解其概率,從而判斷.
的成績有16個,可求解其概率,從而判斷.
(1)設(shè)該名學(xué)生考核成績優(yōu)秀為事件![]() .
.
由莖葉圖中的數(shù)據(jù)可以知道,30名同學(xué)中,有7名同學(xué)考核優(yōu)秀.
所以所求概率![]() 約為
約為![]() .
.
(2)![]() 的所有可能取值為0,1,2,3.
的所有可能取值為0,1,2,3.
因為成績![]() 的學(xué)生共有8人,其中滿足
的學(xué)生共有8人,其中滿足![]() 的學(xué)生有5人.
的學(xué)生有5人.
所以![]() ,
,![]() .
.
![]() ,
,![]() .
.
隨機(jī)變量![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.
(3)根據(jù)表格中的數(shù)據(jù),滿足![]() 的成績有16個.
的成績有16個.
所以![]() .
.
所以可以認(rèn)為此次冰雪培訓(xùn)活動有效.


 課時掌控隨堂練習(xí)系列答案
課時掌控隨堂練習(xí)系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學(xué)業(yè)水平測試系列答案
浙江之星學(xué)業(yè)水平測試系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,圓
中,圓![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以直角坐標(biāo)系的原點(diǎn)
為參數(shù)),以直角坐標(biāo)系的原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系.
軸正半軸為極軸建立極坐標(biāo)系.
(1)求圓![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)設(shè)曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,曲線
,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,求三條曲線
,求三條曲線![]() ,
,![]() ,
,![]() 所圍成圖形的面積.
所圍成圖形的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() ,
,![]() 、
、![]() 為橢圓的左、右焦點(diǎn),
為橢圓的左、右焦點(diǎn),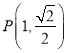 為橢圓上一點(diǎn),且
為橢圓上一點(diǎn),且![]() .
.
(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)設(shè)直線![]() ,過點(diǎn)
,過點(diǎn)![]() 的直線交橢圓于
的直線交橢圓于![]() 、
、![]() 兩點(diǎn),線段
兩點(diǎn),線段![]() 的垂直平分線分別交直線
的垂直平分線分別交直線![]() 、直線
、直線![]() 于
于![]() 、
、![]() 兩點(diǎn),當(dāng)
兩點(diǎn),當(dāng)![]() 最小時,求直線
最小時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
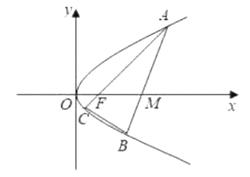
【題目】已知拋物線L:![]() (
(![]() )的焦點(diǎn)為F,過點(diǎn)
)的焦點(diǎn)為F,過點(diǎn)![]() 的動直線l與拋物線L交于A,B兩點(diǎn),直線
的動直線l與拋物線L交于A,B兩點(diǎn),直線![]() 交拋物線L于另一點(diǎn)C,直線
交拋物線L于另一點(diǎn)C,直線![]() 的最小值為4.
的最小值為4.
(1)求橢圓C的方程;
(2)若過點(diǎn)A作y軸的垂線m,則x軸上是否存在一點(diǎn)![]() ,使得直線PB與直線m的交點(diǎn)恒在一條定直線上?若存在,求該點(diǎn)的坐標(biāo)及該定直線的方程;若不存在,請說明理由.
,使得直線PB與直線m的交點(diǎn)恒在一條定直線上?若存在,求該點(diǎn)的坐標(biāo)及該定直線的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在某地區(qū)某高傳染性病毒流行期間,為了建立指標(biāo)顯示疫情已受控制,以便向該地區(qū)居民顯示可以過正常生活,有公共衛(wèi)生專家建議的指標(biāo)是“連續(xù)7天每天新增感染人數(shù)不超過5人”,根據(jù)連續(xù)7天的新增病例數(shù)計算,下列各個選項中,一定符合上述指標(biāo)的是__________.
①平均數(shù)![]() ; ②標(biāo)準(zhǔn)差
; ②標(biāo)準(zhǔn)差![]() ; ③平均數(shù)
; ③平均數(shù)![]() 且標(biāo)準(zhǔn)差
且標(biāo)準(zhǔn)差![]() ;
;
④平均數(shù)![]() 且極差小于或等于2; ⑤眾數(shù)等于1且極差小于或等于4.
且極差小于或等于2; ⑤眾數(shù)等于1且極差小于或等于4.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)有甲、乙兩套設(shè)備生產(chǎn)同一種產(chǎn)品,為了檢測兩套設(shè)備的生產(chǎn)質(zhì)量情況,隨機(jī)從兩套設(shè)備生產(chǎn)的大量產(chǎn)品中各抽取了50件產(chǎn)品作為樣本,檢測一項質(zhì)量指標(biāo)值,若該項質(zhì)量指標(biāo)值落在![]() 內(nèi),則為合格品,否則為不合格品. 表1是甲套設(shè)備的樣本的頻數(shù)分布表,圖1是乙套設(shè)備的樣本的頻率分布直方圖.
內(nèi),則為合格品,否則為不合格品. 表1是甲套設(shè)備的樣本的頻數(shù)分布表,圖1是乙套設(shè)備的樣本的頻率分布直方圖.
表1:甲套設(shè)備的樣本的頻數(shù)分布表
質(zhì)量指標(biāo)值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數(shù) | 1 | 5 | 18 | 19 | 6 | 1 |
圖1:乙套設(shè)備的樣本的頻率分布直方圖
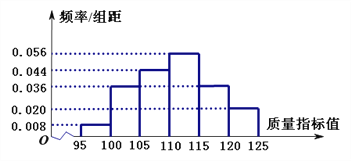
(Ⅰ)將頻率視為概率. 若乙套設(shè)備生產(chǎn)了5000件產(chǎn)品,則其中的不合格品約有多少件;
(Ⅱ)填寫下面列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有90%的把握認(rèn)為該企業(yè)生產(chǎn)的這種產(chǎn)品的質(zhì)量指標(biāo)值與甲、乙兩套設(shè)備的選擇有關(guān);
甲套設(shè)備 | 乙套設(shè)備 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
(Ⅲ)根據(jù)表1和圖1,對兩套設(shè)備的優(yōu)劣進(jìn)行比較.
附:

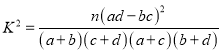 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解戶籍性別對生育二胎選擇傾向的影響,某地從育齡人群中隨機(jī)抽取了容量為![]() 的調(diào)查樣本,其中城鎮(zhèn)戶籍與農(nóng)民戶籍各
的調(diào)查樣本,其中城鎮(zhèn)戶籍與農(nóng)民戶籍各![]() 人;男性
人;男性![]() 人,女性
人,女性![]() 人.繪制不同群體中傾向選擇生育二胎與傾向選擇不生育二胎的人數(shù)比例圖(如圖所示),其中陰影部分表示傾向選擇生育二胎的對應(yīng)比例,則下列敘述中錯誤的是( )
人.繪制不同群體中傾向選擇生育二胎與傾向選擇不生育二胎的人數(shù)比例圖(如圖所示),其中陰影部分表示傾向選擇生育二胎的對應(yīng)比例,則下列敘述中錯誤的是( )
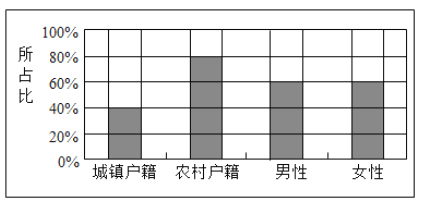
A.是否傾向選擇生育二胎與戶籍有關(guān)
B.是否傾向選擇生育二胎與性別無關(guān)
C.傾向選擇生育二胎的人員中,男性人數(shù)與女性人數(shù)相同
D.傾向選擇不生育二胎的人員中,農(nóng)村戶籍人數(shù)少于城鎮(zhèn)戶籍人數(shù)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 是菱形,四邊形
是菱形,四邊形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 為線段
為線段![]() 上的一點(diǎn).
上的一點(diǎn).
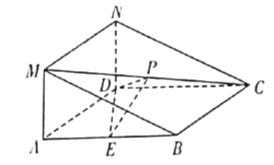
(1)求證:![]() ;
;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() .直線
.直線![]() 被稱作為橢圓
被稱作為橢圓![]() 的一條準(zhǔn)線.點(diǎn)
的一條準(zhǔn)線.點(diǎn)![]() 在橢圓
在橢圓![]() 上(異于橢圓左、右頂點(diǎn)),過點(diǎn)
上(異于橢圓左、右頂點(diǎn)),過點(diǎn)![]() 作直線
作直線![]() 與橢圓
與橢圓![]() 相切,且與直線
相切,且與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() .
.
(1)求證:![]() .
.
(2)若點(diǎn)![]() 在
在![]() 軸的上方,
軸的上方,![]() ,求
,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com