
【題目】函數(shù)f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ< ![]() )的圖象與y軸的交點(diǎn)為(0,
)的圖象與y軸的交點(diǎn)為(0, ![]() ),它的一個(gè)對(duì)稱中心是M(
),它的一個(gè)對(duì)稱中心是M( ![]() ,0),點(diǎn)M與最近的一條對(duì)稱軸的距離是
,0),點(diǎn)M與最近的一條對(duì)稱軸的距離是 ![]() .
.
(1)求此函數(shù)的解析式;
(2)求此函數(shù)取得最大值時(shí)x的取值集合;
(3)當(dāng)x∈(0,π)時(shí),求此函數(shù)的單調(diào)遞增區(qū)間.
【答案】
(1)解:函數(shù)f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ< ![]() )的圖象
)的圖象
的一個(gè)對(duì)稱中心是M( ![]() ,0),點(diǎn)M與最近的一條對(duì)稱軸的距離是
,0),點(diǎn)M與最近的一條對(duì)稱軸的距離是 ![]() ,故
,故  ,
,
求得ω=2,φ= ![]() .
.
再根據(jù)函數(shù)的圖象與y軸的交點(diǎn)為(0, ![]() ),可得Asin(ω0+
),可得Asin(ω0+ ![]() )=
)= ![]() ,∴A=2,
,∴A=2,
函數(shù)f(x)=2sin(2x+ ![]() ).
).
(2)解:令2x+ ![]() =2kπ+
=2kπ+ ![]() ,求得 x=kπ+
,求得 x=kπ+ ![]() ,k∈Z,故函數(shù)取得最大值時(shí)x的取值集合為{x|x=kπ+
,k∈Z,故函數(shù)取得最大值時(shí)x的取值集合為{x|x=kπ+ ![]() ,k∈Z}
,k∈Z}
(3)解:令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,可得函數(shù)的增區(qū)間為[2kπ﹣
,可得函數(shù)的增區(qū)間為[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z.
],k∈Z.
再結(jié)合x(chóng)∈(0,π),可得函數(shù)的增區(qū)間為(0, ![]() ]、[
]、[ ![]() ,π)
,π)
【解析】(1)由函數(shù)的周期性、圖象的對(duì)稱性求出ω、φ的值,由特殊點(diǎn)的坐標(biāo)求出A的值,可得函數(shù)的解析式.(2)利用正弦函數(shù)的最大值,求得函數(shù)取得最大值時(shí)x的取值集合.(3)利用正弦函數(shù)的調(diào)增區(qū)間,求得當(dāng)x∈(0,π)時(shí),此函數(shù)的單調(diào)遞增區(qū)間.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,我國(guó)南海某處的一個(gè)圓形海域上有四個(gè)小島,小島B與小島A、小島C相距都為5n mile,與小島D相距為 ![]() n mile.小島A對(duì)小島B與D的視角為鈍角,且
n mile.小島A對(duì)小島B與D的視角為鈍角,且 ![]() .
.
(Ⅰ)求小島A與小島D之間的距離和四個(gè)小島所形成的四邊形的面積;
(Ⅱ)記小島D對(duì)小島B與C的視角為α,小島B對(duì)小島C與D的視角為β,求sin(2α+β)的值.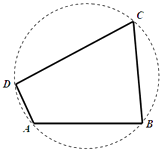
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,已知長(zhǎng)方體ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的點(diǎn),且BE⊥B1C.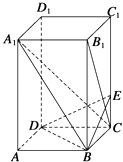
(1)求CE的長(zhǎng);
(2)求證:A1C⊥平面BED;
(3)求A1B與平面BDE夾角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】以下命題中,正確命題的序號(hào)是 . ①函數(shù)y=tanx在定義域內(nèi)是增函數(shù);
②函數(shù)y=2sin(2x+ ![]() )的圖象關(guān)于x=
)的圖象關(guān)于x= ![]() 成軸對(duì)稱;
成軸對(duì)稱;
③已知 ![]() =(3,4),
=(3,4), ![]()
![]() =﹣2,則向量
=﹣2,則向量 ![]() 在向量
在向量 ![]() 的方向上的投影是﹣
的方向上的投影是﹣ ![]()
④如果函數(shù)f(x)=ax2﹣2x﹣3在區(qū)間(﹣∞,4)上是單調(diào)遞減的,則實(shí)數(shù)a的取值范圍是(0, ![]() ].
].
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】現(xiàn)有一塊大型的廣告宣傳版面,其形狀如圖所示的直角梯形![]() .某廠家因產(chǎn)品宣傳的需要,擬出資規(guī)劃出一塊區(qū)域(圖中陰影部分)為產(chǎn)品做廣告,形狀為直角梯形
.某廠家因產(chǎn)品宣傳的需要,擬出資規(guī)劃出一塊區(qū)域(圖中陰影部分)為產(chǎn)品做廣告,形狀為直角梯形![]() (點(diǎn)
(點(diǎn)![]() 在曲線段
在曲線段![]() 上,點(diǎn)
上,點(diǎn)![]() 在線段
在線段![]() 上).已知
上).已知![]() ,
,![]() ,其中曲線段
,其中曲線段![]() 是以
是以![]() 為頂點(diǎn),
為頂點(diǎn),![]() 為對(duì)稱軸的拋物線的一部分.
為對(duì)稱軸的拋物線的一部分.

(1)求線段![]() ,線段
,線段![]() ,曲線段
,曲線段![]() 所圍成區(qū)域的面積;
所圍成區(qū)域的面積;
(2)求廠家廣告區(qū)域![]() 的最大面積.
的最大面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】將邊長(zhǎng)為![]() 的等邊
的等邊![]() 沿
沿![]() 軸正方向滾動(dòng),某時(shí)刻
軸正方向滾動(dòng),某時(shí)刻![]() 與坐標(biāo)原點(diǎn)重合(如圖),設(shè)頂點(diǎn)
與坐標(biāo)原點(diǎn)重合(如圖),設(shè)頂點(diǎn)![]() 的軌跡方程是
的軌跡方程是![]() ,關(guān)于函數(shù)
,關(guān)于函數(shù)![]() 有下列說(shuō)法:
有下列說(shuō)法:

(1)![]() 的值域?yàn)?/span>
的值域?yàn)?/span>![]() ;
;
(2)![]() 是周期函數(shù)且周期為
是周期函數(shù)且周期為![]() ;
;
(3)![]() ;
;
(4)滾動(dòng)后,當(dāng)頂點(diǎn)![]() 第一次落在
第一次落在![]() 軸上時(shí),
軸上時(shí),![]() 的圖象與
的圖象與![]() 軸所圍成的面積為
軸所圍成的面積為![]()
其中正確命題的序號(hào)是__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為得到函數(shù) ![]() 的圖象,只需將函數(shù)y=sin2x的圖象( )
的圖象,只需將函數(shù)y=sin2x的圖象( )
A.向左平移 ![]() 個(gè)長(zhǎng)度單位
個(gè)長(zhǎng)度單位
B.向右平移 ![]() 個(gè)長(zhǎng)度單位
個(gè)長(zhǎng)度單位
C.向左平移 ![]() 個(gè)長(zhǎng)度單位
個(gè)長(zhǎng)度單位
D.向右平移 ![]() 個(gè)長(zhǎng)度單位
個(gè)長(zhǎng)度單位
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() 是由
是由![]() 個(gè)有序?qū)崝?shù)構(gòu)成的一個(gè)數(shù)組,記作
個(gè)有序?qū)崝?shù)構(gòu)成的一個(gè)數(shù)組,記作![]() ,其中
,其中![]()
![]()
![]() 稱為數(shù)組
稱為數(shù)組![]() 的“元”,
的“元”, ![]() 稱為
稱為![]() 的下標(biāo),如果數(shù)組
的下標(biāo),如果數(shù)組![]() 中的每個(gè)“元”都是來(lái)自數(shù)組
中的每個(gè)“元”都是來(lái)自數(shù)組
![]() 中不同下標(biāo)的“元”,則稱
中不同下標(biāo)的“元”,則稱![]() 為
為![]() 的子數(shù)組,定義兩個(gè)數(shù)組
的子數(shù)組,定義兩個(gè)數(shù)組![]() 和
和![]()
![]() 的關(guān)系數(shù)為
的關(guān)系數(shù)為![]() ;
;
(1)若![]() ,
, ![]() ,設(shè)
,設(shè)![]() 是
是![]() 的含有兩個(gè)“元”的子數(shù)組,求
的含有兩個(gè)“元”的子數(shù)組,求![]()
的最大值;
(2)若 ,
, ![]() ,且
,且![]() ,
, ![]() 為
為![]() 的含有三個(gè)“元”
的含有三個(gè)“元”
的子數(shù)組,求![]() 的最大值;
的最大值;
(3)若數(shù)組![]() 中的“元”滿足
中的“元”滿足![]() ,設(shè)數(shù)組
,設(shè)數(shù)組![]()
![]() 含有
含有
四個(gè)“元”![]() ,且
,且![]() ,求
,求![]() 與
與![]() 的所有含有三個(gè)“元”
的所有含有三個(gè)“元”
的子數(shù)組的關(guān)系數(shù)的最大值;
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(文)已知點(diǎn)D(1, ![]() )在雙曲線C:
)在雙曲線C: ![]() =1(a>0,b>0)上,且雙曲線的一條漸近線的方程是
=1(a>0,b>0)上,且雙曲線的一條漸近線的方程是 ![]() x+y=0.
x+y=0.
(1)求雙曲線C的方程;
(2)若過(guò)點(diǎn)(0,1)且斜率為k的直線l與雙曲線C有兩個(gè)不同交點(diǎn),求實(shí)數(shù)k的取值范圍;
(3)設(shè)(2)中直線l與雙曲線C交于A、B兩個(gè)不同點(diǎn),若以線段AB為直徑的圓經(jīng)過(guò)坐標(biāo)原點(diǎn),求實(shí)數(shù)k的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com